5. (8分)某窗户的形状如图6所示,其中上部是半径为$x\space cm$的半圆,下部是长为$y\space cm$的长方形。
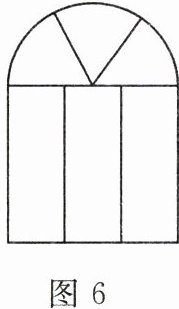
(1)用含$x$,$y的代数式表示窗户的面积S$;
(2)当$x= 40$,$y= 120$时,求窗户的面积$S$。

(1)用含$x$,$y的代数式表示窗户的面积S$;
(2)当$x= 40$,$y= 120$时,求窗户的面积$S$。
答案:
(1) 因为半圆的半径为 $ x\space cm $,所以长方形的宽为 $ 2x\space cm $。
窗户面积 $ S = $ 半圆面积 $ + $ 长方形面积,
即 $ S = \frac{1}{2}\pi x^2 + 2x \cdot y $。
(2) 当 $ x = 40 $,$ y = 120 $ 时,
$ S = \frac{1}{2}\pi × 40^2 + 2 × 40 × 120 $
$ = \frac{1}{2}\pi × 1600 + 9600 $
$ = 800\pi + 9600 $。
答:窗户的面积 $ S $ 为 $ (800\pi + 9600)\space cm^2 $。
(1) 因为半圆的半径为 $ x\space cm $,所以长方形的宽为 $ 2x\space cm $。
窗户面积 $ S = $ 半圆面积 $ + $ 长方形面积,
即 $ S = \frac{1}{2}\pi x^2 + 2x \cdot y $。
(2) 当 $ x = 40 $,$ y = 120 $ 时,
$ S = \frac{1}{2}\pi × 40^2 + 2 × 40 × 120 $
$ = \frac{1}{2}\pi × 1600 + 9600 $
$ = 800\pi + 9600 $。
答:窗户的面积 $ S $ 为 $ (800\pi + 9600)\space cm^2 $。
6. (8分)物体自由下落的高度$h(m)和下落时间t(s)$的关系,在地球上大约是:$h= 4.9t^{2}$,在月球上大约是:$h= 0.8t^{2}$。
(1)填写下表:
| $t$ | 0 | 2 | 4 | 6 | 8 | 10 |
| $h= 4.9t^{2}$ |
| $h= 0.8t^{2}$ |

(2)物体在哪儿下落得快?
(1)填写下表:
| $t$ | 0 | 2 | 4 | 6 | 8 | 10 |
| $h= 4.9t^{2}$ |
0
| 19.6
| 78.4
| 176.4
| 313.6
| 490
|| $h= 0.8t^{2}$ |
0
| 3.2
| 12.8
| 28.8
| 51.2
| 80
|
(2)物体在哪儿下落得快?
地球
答案:
(1)
| $t$ | 0 | 2 | 4 | 6 | 8 | 10 |
| $h=4.9t^{2}$ | 0 | 19.6 | 78.4 | 176.4 | 313.6 | 490 |
| $h=0.8t^{2}$ | 0 | 3.2 | 12.8 | 28.8 | 51.2 | 80 |
(2) 地球
(1)
| $t$ | 0 | 2 | 4 | 6 | 8 | 10 |
| $h=4.9t^{2}$ | 0 | 19.6 | 78.4 | 176.4 | 313.6 | 490 |
| $h=0.8t^{2}$ | 0 | 3.2 | 12.8 | 28.8 | 51.2 | 80 |
(2) 地球
用同样规格的黑、白两种颜色的正方形瓷砖,按如图7所示的方式铺地面:
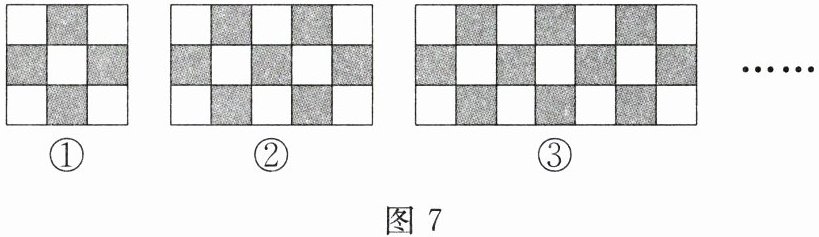
(1)观察图形,填写下表:
| 图形 | ① | ② | ③ | …$$ |
| 黑色瓷砖的块数 | 4 | 7 |
| 黑、白两种瓷砖的总块数 | 9 | 15 |

(2)推测第$n$个图形中黑色瓷砖的块数为
(3)白色瓷砖与黑色瓷砖的总块数可能是2024吗?若可能,求出是第几个图形;若不可能,请说明理由。
不可能。
设白色瓷砖有$x$块,由(2)可知黑色瓷砖有$(3n + 1)$块,黑、白两种瓷砖总块数为$(6n + 3)$块,则$x+(3n + 1)=6n + 3$,解得$x = 3n + 2$。
若黑、白瓷砖总块数是$2024$,即$6n + 3 = 2024$,$6n=2021$,$n=\frac{2021}{6}$,不是整数,所以不可能。

(1)观察图形,填写下表:
| 图形 | ① | ② | ③ | …$$ |
| 黑色瓷砖的块数 | 4 | 7 |
10
| …$$ || 黑、白两种瓷砖的总块数 | 9 | 15 |
21
| …$$ |
(2)推测第$n$个图形中黑色瓷砖的块数为
$3n + 1$
,黑、白两种瓷砖的总块数为$6n + 3$
(用含$n$的代数式表示);(3)白色瓷砖与黑色瓷砖的总块数可能是2024吗?若可能,求出是第几个图形;若不可能,请说明理由。
不可能。
设白色瓷砖有$x$块,由(2)可知黑色瓷砖有$(3n + 1)$块,黑、白两种瓷砖总块数为$(6n + 3)$块,则$x+(3n + 1)=6n + 3$,解得$x = 3n + 2$。
若黑、白瓷砖总块数是$2024$,即$6n + 3 = 2024$,$6n=2021$,$n=\frac{2021}{6}$,不是整数,所以不可能。
答案:
(1)
| 图形 | ① | ② | ③ | … |
| --- | --- | --- | --- | --- |
| 黑色瓷砖的块数 | 4 | 7 | 10 | … |
| 黑、白两种瓷砖的总块数 | 9 | 15 | 21 | … |
(2)$3n + 1$;$6n + 3$
(3)不可能。
设白色瓷砖有$x$块,由(2)可知黑色瓷砖有$(3n + 1)$块,黑、白两种瓷砖总块数为$(6n + 3)$块,则$x+(3n + 1)=6n + 3$,解得$x = 3n + 2$。
若黑、白瓷砖总块数是$2024$,即$6n + 3+ (3n + 2)- (3n + 2)(白色瓷砖表达式代入总瓷砖数中,总瓷砖数就是黑瓷砖与白瓷砖之和)= 6n + 3 = 2024$(这里直接用总瓷砖数表达式),$6n+3 = 2024$,$6n=2021$,$n=\frac{2021}{6}$,不是整数,所以不可能。
| 图形 | ① | ② | ③ | … |
| --- | --- | --- | --- | --- |
| 黑色瓷砖的块数 | 4 | 7 | 10 | … |
| 黑、白两种瓷砖的总块数 | 9 | 15 | 21 | … |
(2)$3n + 1$;$6n + 3$
(3)不可能。
设白色瓷砖有$x$块,由(2)可知黑色瓷砖有$(3n + 1)$块,黑、白两种瓷砖总块数为$(6n + 3)$块,则$x+(3n + 1)=6n + 3$,解得$x = 3n + 2$。
若黑、白瓷砖总块数是$2024$,即$6n + 3+ (3n + 2)- (3n + 2)(白色瓷砖表达式代入总瓷砖数中,总瓷砖数就是黑瓷砖与白瓷砖之和)= 6n + 3 = 2024$(这里直接用总瓷砖数表达式),$6n+3 = 2024$,$6n=2021$,$n=\frac{2021}{6}$,不是整数,所以不可能。
查看更多完整答案,请扫码查看


