9. 已知$m$是两位数,$n$是一位数,把$m直接写在n$后面,就成为一个三位数,这个三位数可表示成(
A.$10n+m$
B.$nm$
C.$100n+m$
D.$100m+n$
C
)A.$10n+m$
B.$nm$
C.$100n+m$
D.$100m+n$
答案:
C
10. 如图2,这是一个运算程序,若第1次输入$a$的值为16,则第2024次输出的结果是(
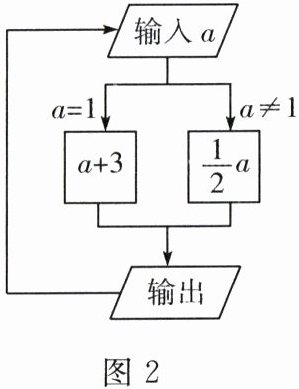
A.1
B.3
C.4
D.8
C
)
A.1
B.3
C.4
D.8
答案:
C
1. “比$a$的2倍大1的数”用代数式表示是
$2a + 1$
。
答案:
$2a + 1$
2. 若$a$与2互为相反数,则$a+1= $
-1
。
答案:
-1
3. “$m的\frac{1}{3}与n$的2倍的和”用代数式表示为
$\frac{1}{3}m + 2n$
。
答案:
$\frac{1}{3}m + 2n$
4. 如果一个三位数百位数字是$a$,十位数字是0,个位数字是$b$,则这三位数用代数式表示为
100a + b
。
答案:
100a + b
5. 两个量$x和y$成反比例,如果当$x= 2$时,$y= 5$,那么当$y= \frac{2}{3}$时,$x= $
15
。
答案:
15
6. 若$|a+2|+(b-3)^{2}= 0$,则$(a+b+1)×(2-\frac{b}{a})$的值是
7
。
答案:
7(题目是填空题,直接填数值)
7. 已知$|3x-6|+(y+3)^{2}= 0$,则$3x+2y$的值是
0
。
答案:
0
8. “人间四月芳菲尽,山寺桃花始盛开。”某地区夏季高山上的温度从山脚处开始每升高100m降低$0.6^{\circ}C$。若山脚温度为$20^{\circ}C$,则比山脚高$x\space m$处的温度为
$20 - 0.006x$
$^{\circ}C$。
答案:
$20 - 0.006x$
9. 一个棱长为$a$的正方体铁块,被锻造成一个底面半径为$r$的圆柱形零件,则这个零件的高$h= $
$\frac{a^3}{\pi r^2}$
;当$a= 3$,$r= 2$时,$h= $$2.25$(或$\frac{9}{4}$)
($\pi$取3)。
答案:
$\frac{a^3}{\pi r^2}$;$2.25$(或$\frac{9}{4}$)
10. 按如图3所示的方法用小棒摆正六边形,摆2个正六边形要11根小棒,摆3个正六边形要16根小棒,摆$n$个正六边形需要
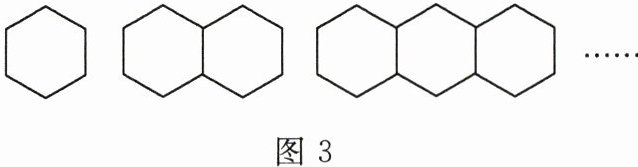
$5n + 1$
根小棒。
答案:
$5n + 1$
1. (3分)根据所给的字母的值,求下列代数式的值:当$x= -1$,$\frac{1}{2}$时,分别求代数式$4x^{3}-x^{2}+1$的值。
答案:
当$x = -1$时,
$\begin{aligned}4x^{3}-x^{2}+1&=4×(-1)^{3}-(-1)^{2}+1\\&=4×(-1)-1 + 1\\&=-4 - 1 + 1\\&=-4\end{aligned}$
当$x=\frac{1}{2}$时,
$\begin{aligned}4x^{3}-x^{2}+1&=4×\left(\frac{1}{2}\right)^{3}-\left(\frac{1}{2}\right)^{2}+1\\&=4×\frac{1}{8}-\frac{1}{4}+1\\&=\frac{1}{2}-\frac{1}{4}+1\\&=\frac{1}{4}+1\\&=\frac{5}{4}\end{aligned}$
结论:当$x=-1$时,代数式的值为$-4$;当$x=\frac{1}{2}$时,代数式的值为$\frac{5}{4}$。
$\begin{aligned}4x^{3}-x^{2}+1&=4×(-1)^{3}-(-1)^{2}+1\\&=4×(-1)-1 + 1\\&=-4 - 1 + 1\\&=-4\end{aligned}$
当$x=\frac{1}{2}$时,
$\begin{aligned}4x^{3}-x^{2}+1&=4×\left(\frac{1}{2}\right)^{3}-\left(\frac{1}{2}\right)^{2}+1\\&=4×\frac{1}{8}-\frac{1}{4}+1\\&=\frac{1}{2}-\frac{1}{4}+1\\&=\frac{1}{4}+1\\&=\frac{5}{4}\end{aligned}$
结论:当$x=-1$时,代数式的值为$-4$;当$x=\frac{1}{2}$时,代数式的值为$\frac{5}{4}$。
查看更多完整答案,请扫码查看


