第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
例2
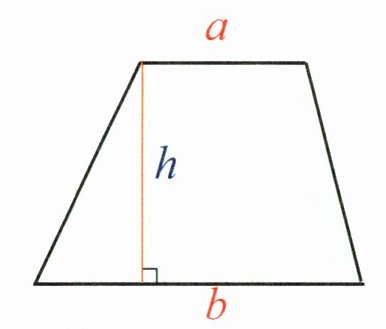
如图,用字母S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,梯形的面积公式可表示为:

如图,用字母S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,梯形的面积公式可表示为:
$S= (a+b)h÷2$
.
答案:
解析:本题考查梯形面积公式的推导。
答案:
$S=(a+b)h÷2$。
答案:
$S=(a+b)h÷2$。
小探究
还可以用什么方法来推导梯形的面积公式?
我把梯形分割成两个三角形来计算.
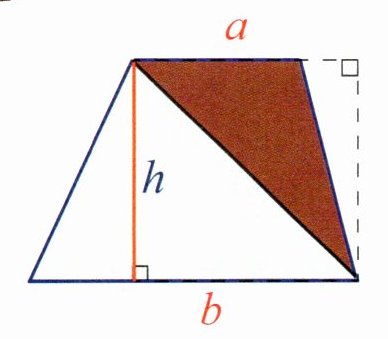
两个三角形的面积分别为:
梯形的面积=
你是怎么算的?
还可以用什么方法来推导梯形的面积公式?
我把梯形分割成两个三角形来计算.

两个三角形的面积分别为:
$\frac{1}{2}ah$
,$\frac{1}{2}bh$
,梯形的面积=
$\frac{1}{2}(a + b)h$
.你是怎么算的?
把梯形分割成两个三角形,一个三角形底为上底$a$,高为梯形的高$h$,根据三角形面积公式$S=\frac{1}{2}ah$算出其面积为$\frac{1}{2}ah$;另一个三角形底为下底$b$,高为梯形的高$h$,算出其面积为$\frac{1}{2}bh$,将两个三角形面积相加就得到梯形面积$\frac{1}{2}ah+\frac{1}{2}bh=\frac{1}{2}(a + b)h$。
答案:
解析:本题主要考查梯形面积公式的推导,通过将梯形分割成两个三角形,利用三角形面积公式分别求出两个三角形面积,再将它们相加得到梯形面积。
三角形面积公式为$S = \frac{1}{2}ah$($a$为底,$h$为高)。
对于梯形分割成的两个三角形,一个三角形以梯形的上底$a$为底,梯形的高$h$为高,根据三角形面积公式,其面积为$\frac{1}{2}ah$;另一个三角形以梯形的下底$b$为底,梯形的高$h$为高,其面积为$\frac{1}{2}bh$。
梯形面积等于这两个三角形面积之和,即$\frac{1}{2}ah+\frac{1}{2}bh$,提取公因式$\frac{1}{2}h$可得$\frac{1}{2}(a + b)h$。
答案:$\frac{1}{2}ah$;$\frac{1}{2}bh$;$\frac{1}{2}(a + b)h$;把梯形分割成两个三角形,一个三角形底为上底$a$,高为梯形的高$h$,根据三角形面积公式$S=\frac{1}{2}ah$算出其面积为$\frac{1}{2}ah$;另一个三角形底为下底$b$,高为梯形的高$h$,算出其面积为$\frac{1}{2}bh$,将两个三角形面积相加就得到梯形面积$\frac{1}{2}ah+\frac{1}{2}bh=\frac{1}{2}(a + b)h$。
三角形面积公式为$S = \frac{1}{2}ah$($a$为底,$h$为高)。
对于梯形分割成的两个三角形,一个三角形以梯形的上底$a$为底,梯形的高$h$为高,根据三角形面积公式,其面积为$\frac{1}{2}ah$;另一个三角形以梯形的下底$b$为底,梯形的高$h$为高,其面积为$\frac{1}{2}bh$。
梯形面积等于这两个三角形面积之和,即$\frac{1}{2}ah+\frac{1}{2}bh$,提取公因式$\frac{1}{2}h$可得$\frac{1}{2}(a + b)h$。
答案:$\frac{1}{2}ah$;$\frac{1}{2}bh$;$\frac{1}{2}(a + b)h$;把梯形分割成两个三角形,一个三角形底为上底$a$,高为梯形的高$h$,根据三角形面积公式$S=\frac{1}{2}ah$算出其面积为$\frac{1}{2}ah$;另一个三角形底为下底$b$,高为梯形的高$h$,算出其面积为$\frac{1}{2}bh$,将两个三角形面积相加就得到梯形面积$\frac{1}{2}ah+\frac{1}{2}bh=\frac{1}{2}(a + b)h$。
试一试
1 求出下列梯形的面积:
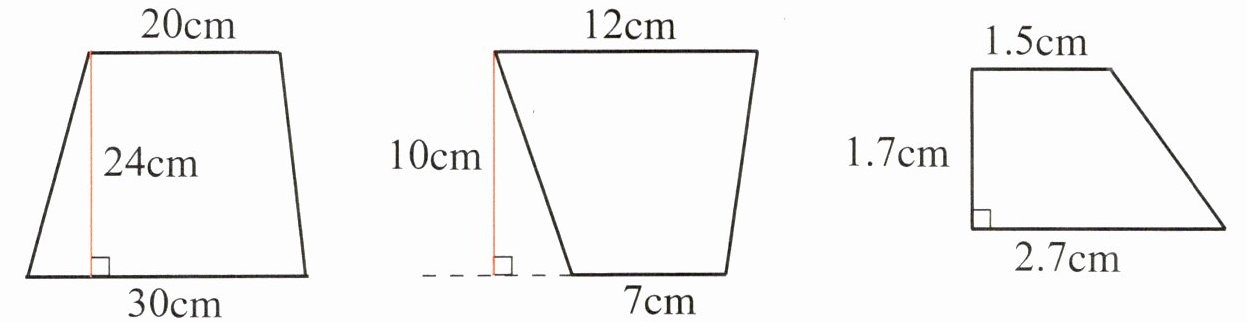
1 求出下列梯形的面积:

答案:
解析:本题考查梯形面积的计算,梯形的面积公式为$S=(a + b)h÷2$(其中$a$为上底,$b$为下底,$h$为高)。
答案:
第一个梯形:
$S=(20 + 30)×24÷2$
$=50×24÷2$
$=1200÷2$
$= 600$($cm^2$)
第二个梯形:
$S=(12 + 7)×10÷2$
$=19×10÷2$
$=190÷2$
$= 95$($cm^2$)
第三个梯形:
$S=(1.5 + 2.7)×1.7÷2$
$=4.2×1.7÷2$
$=7.14÷2$
$= 3.57$($cm^2$)
综上,三个梯形的面积分别为$600cm^2$、$95cm^2$、$3.57cm^2$。
答案:
第一个梯形:
$S=(20 + 30)×24÷2$
$=50×24÷2$
$=1200÷2$
$= 600$($cm^2$)
第二个梯形:
$S=(12 + 7)×10÷2$
$=19×10÷2$
$=190÷2$
$= 95$($cm^2$)
第三个梯形:
$S=(1.5 + 2.7)×1.7÷2$
$=4.2×1.7÷2$
$=7.14÷2$
$= 3.57$($cm^2$)
综上,三个梯形的面积分别为$600cm^2$、$95cm^2$、$3.57cm^2$。
2 如图,已知一个梯形的面积为$52cm^2$,上底和下底的长分别为5cm和8cm,求这个梯形的高.
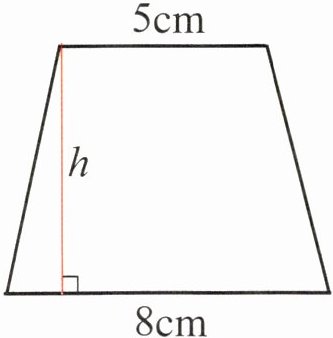

答案:
解析:本题考查梯形面积公式的应用,梯形的面积公式为$S=(a + b)h÷2$(其中$S$表示梯形面积,$a$表示上底,$b$表示下底,$h$表示高),可通过已知的面积、上底和下底来求出梯形的高。
根据梯形面积公式$S=(a + b)h÷2$,可推导出$h = 2S÷(a + b)$。
已知$S = 52cm^2$,$a = 5cm$,$b = 8cm$,将其代入$h = 2S÷(a + b)$可得:
$h=2×52÷(5 + 8)$
$=2×52÷13$
$=104÷13$
$ = 8(cm)$
答案:这个梯形的高为$8cm$。
根据梯形面积公式$S=(a + b)h÷2$,可推导出$h = 2S÷(a + b)$。
已知$S = 52cm^2$,$a = 5cm$,$b = 8cm$,将其代入$h = 2S÷(a + b)$可得:
$h=2×52÷(5 + 8)$
$=2×52÷13$
$=104÷13$
$ = 8(cm)$
答案:这个梯形的高为$8cm$。
查看更多完整答案,请扫码查看


