《2025年教材课本五年级数学上册沪教版54制》

1. 在(28)中填入适当的数.
73 +(28)= 101； 162 -(109)= 53；
23 ×(5)= 115； 32 ÷(4)= 8 .

答案： 解析：本题主要考查基本的四则运算。我们需要通过逆向运算来找出括号中应填入的数字。
对于第一个表达式 73 + ( ) = 101，我们可以通过减法来找到答案：101 - 73 = 28，所以第一个空应填入28。
对于第二个表达式 162 - ( ) = 53，我们可以通过减法来找到答案：162 - 53 = 109，所以第二个空应填入109。
对于第三个表达式 23 × ( ) = 115，我们可以通过除法来找到答案：115 ÷ 23 = 5，所以第三个空应填入5。
对于第四个表达式 32 ÷ ( ) = 8，我们可以通过除法来找到答案：32 ÷ 8 = 4，所以第四个空应填入4。
答案：28；109；5；4。

2. 各式中的■表示什么数?
99.973677

答案： 本题可根据四则运算各部分之间的关系来求解。
1. 计算$28 + ■ = 127.9$中$■$的值
根据“加数=和 - 另一个加数”，可得：
$■=127.9 - 28 = 99.9$
2. 计算$15×■ = 105$中$■$的值
根据“因数=积÷另一个因数”，可得：
$■ = 105÷15 = 7$
3. 计算$■ + ■ = 72$中$■$的值
先将其转化为$2×■ = 72$，再根据“因数=积÷另一个因数”，可得：
$■ = 72÷2 = 36$
4. 计算$■÷7 = 11$中$■$的值
根据“被除数=商×除数”，可得：
$■ = 11×7 = 77$
综上，答案依次为：$99.9$；$7$；$36$；$77$。

3. 各式中的▲表示什么数字?



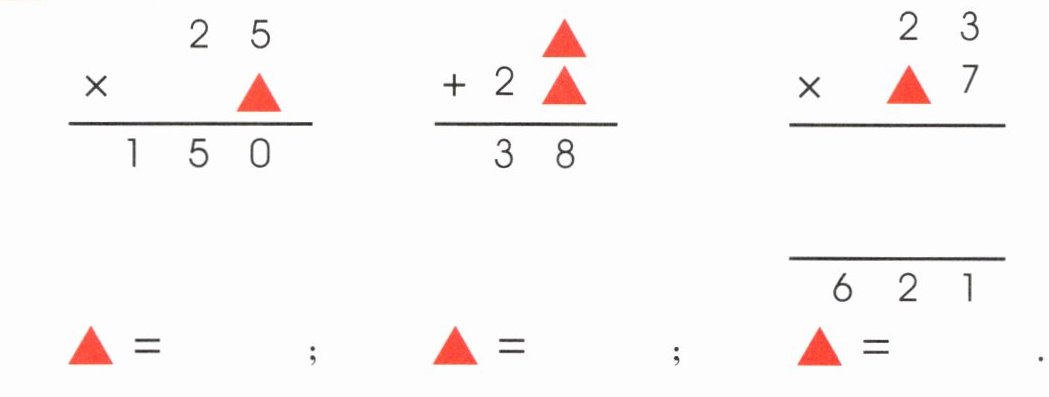
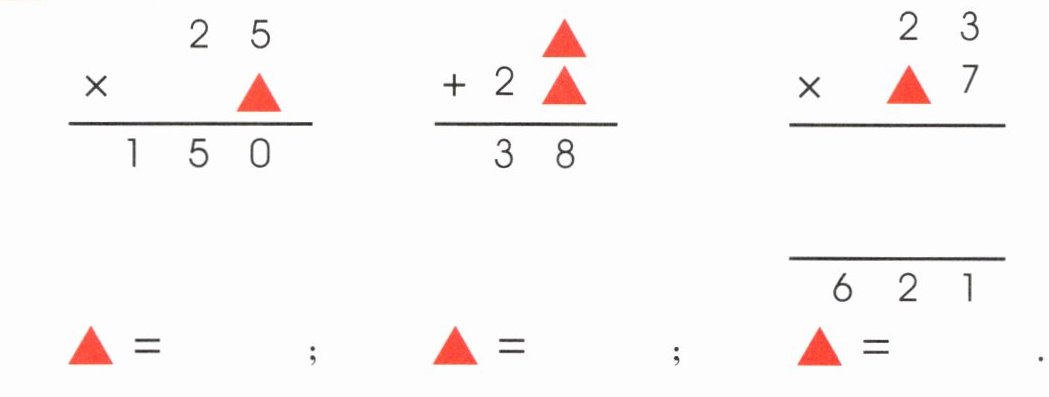
692

答案： 6    9    2

4. 找规律.

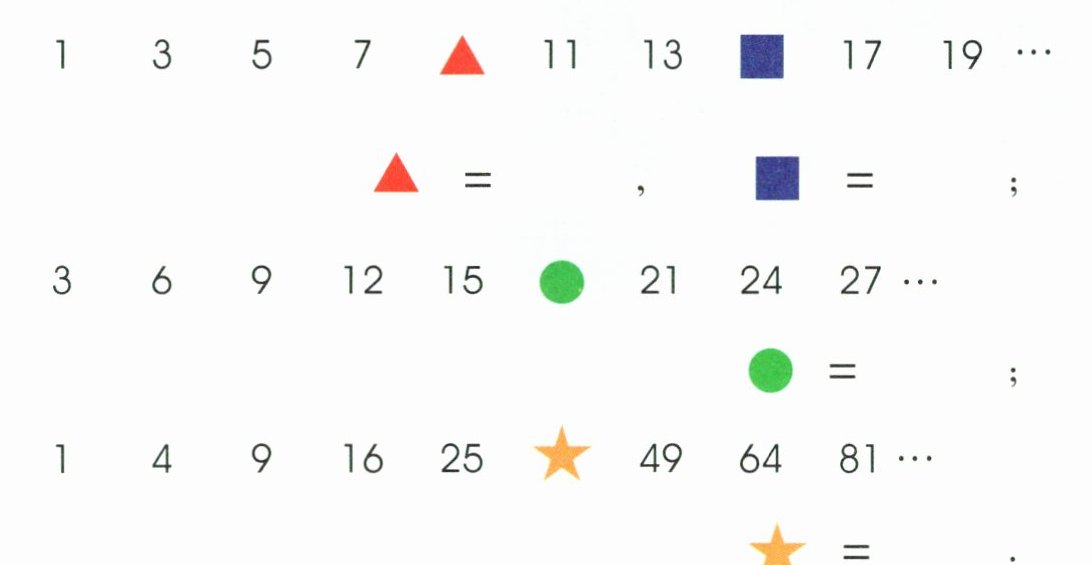
答案： 解析：
本题考察的是数列中的规律识别与运用。
对于第一组数列 1，3，5，7，▲，11，13，■，17，19，…
可以看出这是一个等差数列，差值为2。
因此，▲ = 7 + 2 = 9，■ = 13 + 2 = 15。
对于第二组数列 3，6，9，12，15，●，21，24，27，…
这同样是一个等差数列，差值为3。
因此，● = 15 + 3 = 18。
对于第三组数列 1，4，9，16，25，★，49，64，81，…
观察发现，这些数都是完全平方数，即$ 1^2，$$2^2，$$3^2，$$4^2，$$5^2，$…
因此，$★ = 6^2 = 36。$
答案：
▲ = 9；
■ = 15；
● = 18；
★ = 36。

5. 填空.
① 960 ÷ ◆ ＞ 160,◆可以表示的整数有(1、2、3、4、5).
② $\frac{3}{8} ＜ \frac{3}{●} ＜ \frac{3}{4}$,●可以表示的整数有(5、6、7).

答案： 解析：
①本题可根据除法运算中各部分的关系，结合已知条件求出◆的取值范围，进而确定◆可以表示的整数。
根据“被除数÷除数 = 商”，可得“除数 = 被除数÷商”。
已知$960÷◆\gt160$，则$◆\lt960÷160 = 6$，又因为◆作为除数不能为$0$，且要使$960÷◆$的结果大于$160$，所以◆是大于$0$且小于$6$的整数，即◆可以表示的整数有$1$、$2$、$3$、$4$、$5$。
②本题可根据分子相同的分数比较大小的方法，确定●的取值范围，进而确定●可以表示的整数。
分子相同的分数，分母越小，分数越大。
已知$\frac{3}{8}\lt\frac{3}{●}\lt\frac{3}{4}$，所以$4\lt●\lt8$，那么●可以表示的整数有$5$、$6$、$7$。
答案：
①$1$、$2$、$3$、$4$、$5$；
②$5$、$6$、$7$。