第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
试一试
1 动手做一做
下图中,AC和BD都叫做□ABCD的对角线.沿一条对角线剪开,得到的两个三角形有什么特点?

自己动手做一做.
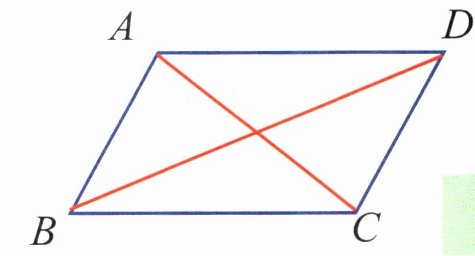
你有什么发现?
沿对角线AC剪开
沿对角线BD剪开
平行四边形的对边相等;平行四边形的对角相等.
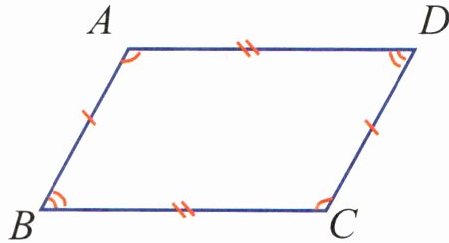
2 小实验
a 如图,用这三根小棍首尾相连围成一个三角形,想一想,同样用这三根小棍还能围成其他形状的三角形吗?
我试了多次,只能围出这一个三角形.
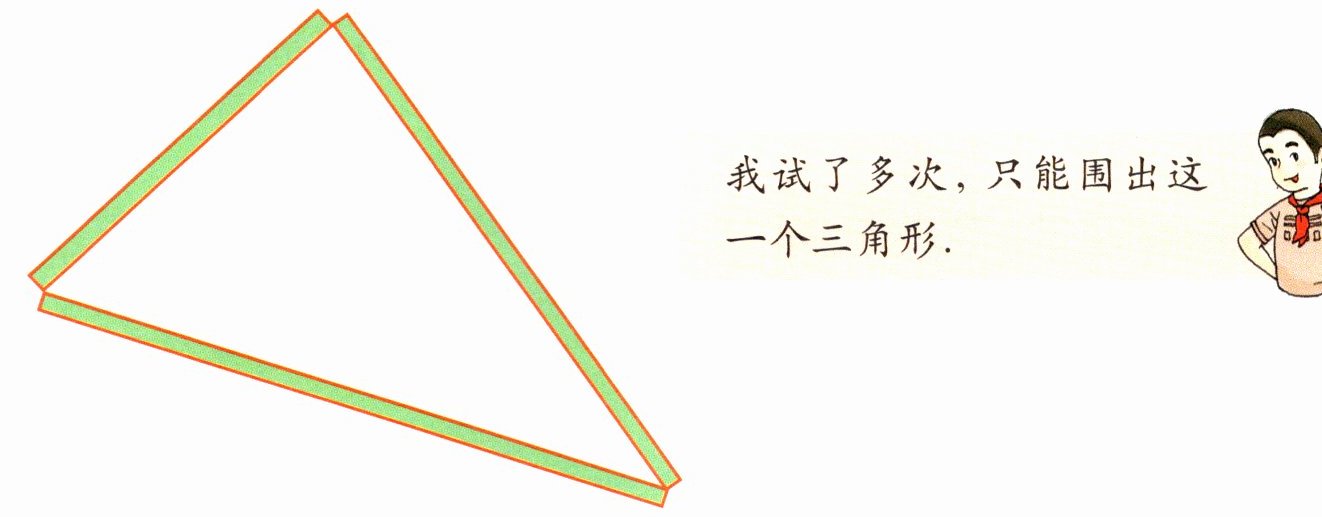
由上可知,三角形的三条边确定了,它的形状、大小也就完全确定了.
b 如图,用四根小棍(其中两根小棍一样长,另外两根小棍也一样长)首尾相连围成一个平行四边形,想一想,同样用这四根小棍还能围成其他形状的平行四边形吗?
我围出了很多不同的平行四边形.
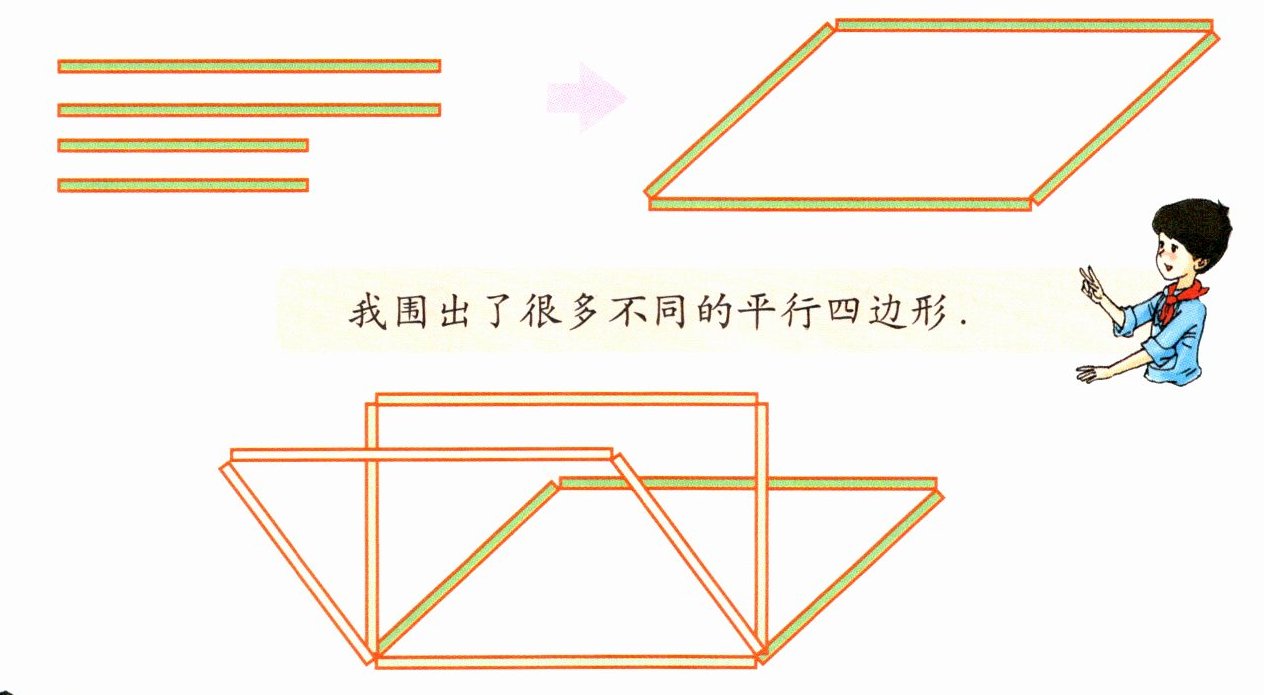
由上可知,平行四边形四条边确定了,它的形状、大小还不能完全确定.
1 动手做一做
下图中,AC和BD都叫做□ABCD的对角线.沿一条对角线剪开,得到的两个三角形有什么特点?

自己动手做一做.

你有什么发现?
沿对角线AC剪开
沿对角线BD剪开
平行四边形的对边相等;平行四边形的对角相等.

2 小实验
a 如图,用这三根小棍首尾相连围成一个三角形,想一想,同样用这三根小棍还能围成其他形状的三角形吗?
我试了多次,只能围出这一个三角形.

由上可知,三角形的三条边确定了,它的形状、大小也就完全确定了.
b 如图,用四根小棍(其中两根小棍一样长,另外两根小棍也一样长)首尾相连围成一个平行四边形,想一想,同样用这四根小棍还能围成其他形状的平行四边形吗?
我围出了很多不同的平行四边形.

由上可知,平行四边形四条边确定了,它的形状、大小还不能完全确定.
答案:
1.
沿对角线$AC$剪开,得到的两个三角形是$\triangle ABC$和$\triangle CDA$,这两个三角形中,$AB = CD$,$BC = DA$(平行四边形对边相等),$\angle B=\angle D$(平行四边形对角相等),$\angle BAC=\angle DCA$,$\angle BCA = \angle DAC$(平行四边形对角相等以及内错角相等),即这两个三角形全等。
沿对角线$BD$剪开,得到的两个三角形是$\triangle ABD$和$\triangle CDB$,这两个三角形中,$AB = CD$,$AD = CB$,$\angle A=\angle C$,$\angle ABD=\angle CDB$,$\angle ADB=\angle CBD$,这两个三角形也全等。
发现:沿平行四边形对角线剪开得到的两个三角形全等。
2. a.
三角形的三条边确定了,它的形状、大小也就完全确定了,这是因为三角形具有稳定性。
b.
平行四边形四条边确定了,它的形状、大小还不能完全确定,这是因为平行四边形具有不稳定性(易变形性),当四条边长度固定时,它的内角大小可以改变,从而形成不同形状的平行四边形。
沿对角线$AC$剪开,得到的两个三角形是$\triangle ABC$和$\triangle CDA$,这两个三角形中,$AB = CD$,$BC = DA$(平行四边形对边相等),$\angle B=\angle D$(平行四边形对角相等),$\angle BAC=\angle DCA$,$\angle BCA = \angle DAC$(平行四边形对角相等以及内错角相等),即这两个三角形全等。
沿对角线$BD$剪开,得到的两个三角形是$\triangle ABD$和$\triangle CDB$,这两个三角形中,$AB = CD$,$AD = CB$,$\angle A=\angle C$,$\angle ABD=\angle CDB$,$\angle ADB=\angle CBD$,这两个三角形也全等。
发现:沿平行四边形对角线剪开得到的两个三角形全等。
2. a.
三角形的三条边确定了,它的形状、大小也就完全确定了,这是因为三角形具有稳定性。
b.
平行四边形四条边确定了,它的形状、大小还不能完全确定,这是因为平行四边形具有不稳定性(易变形性),当四条边长度固定时,它的内角大小可以改变,从而形成不同形状的平行四边形。
查看更多完整答案,请扫码查看


