第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
例1在数学中,我们常用a,b,c,x等字母来表示数.
下图中,字母a,b,c,d,e分别表示数射线上的一些点所对应的数,你知道它们分别表示什么数吗?
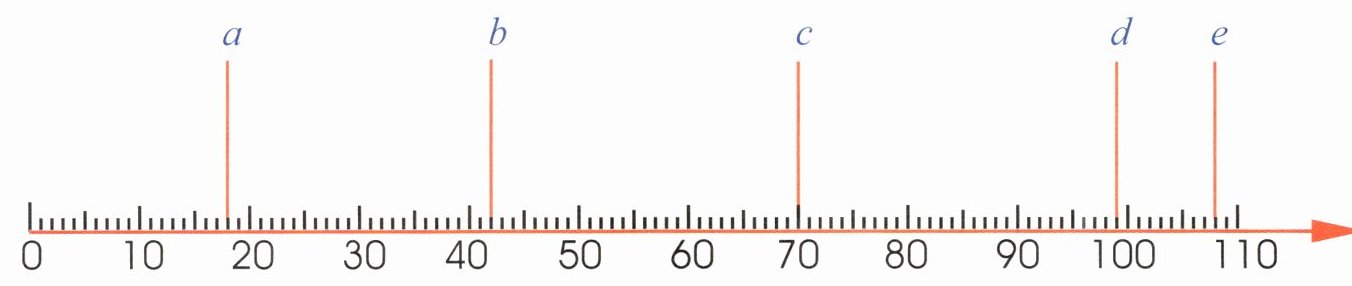
a =
d =
下图中,字母a,b,c,d,e分别表示数射线上的一些点所对应的数,你知道它们分别表示什么数吗?

a =
20
b = 40
c = 70
d =
95
e = 105
答案:
a = 20 b = 40 c = 70
d = 95 e = 105
d = 95 e = 105
例2我们可以用含有字母的式子来表示运算定律和运算性质.
 乘法交换律:$a × b = b × a$.
乘法交换律:$a × b = b × a$.

乘法分配律:$(a + b) × c = a × c + b × c$.
用含有字母的式子表示运算定律有什么好处呢?
在含有字母的式子里,字母与字母之间的乘号可以记作“·”,也可以省略不写.
$a × b = b × a可以写成a \cdot b = b \cdot a或ab = ba$.
$(a + b) × c = a × c + b × c可以写成(a + b) \cdot c = a \cdot c + b \cdot c或(a + b)c = ac + bc$.
你还学过哪些运算定律和运算性质?
请你用含有字母的式子表示出来.
 乘法交换律:$a × b = b × a$.
乘法交换律:$a × b = b × a$.
乘法分配律:$(a + b) × c = a × c + b × c$.
用含有字母的式子表示运算定律有什么好处呢?
在含有字母的式子里,字母与字母之间的乘号可以记作“·”,也可以省略不写.
$a × b = b × a可以写成a \cdot b = b \cdot a或ab = ba$.
$(a + b) × c = a × c + b × c可以写成(a + b) \cdot c = a \cdot c + b \cdot c或(a + b)c = ac + bc$.
你还学过哪些运算定律和运算性质?
请你用含有字母的式子表示出来.
答案:
加法交换律:$a + b = b + a$
加法结合律:$(a + b) + c = a + (b + c)$
乘法结合律:$(a × b) × c = a × (b × c)$或$(ab)c = a(bc)$
减法运算性质:$a - b - c = a - (b + c)$
除法运算性质:$a ÷ b ÷ c = a ÷ (b × c)$($b$、$c$均不为$0$)
加法结合律:$(a + b) + c = a + (b + c)$
乘法结合律:$(a × b) × c = a × (b × c)$或$(ab)c = a(bc)$
减法运算性质:$a - b - c = a - (b + c)$
除法运算性质:$a ÷ b ÷ c = a ÷ (b × c)$($b$、$c$均不为$0$)
查看更多完整答案,请扫码查看


