《2025年暑假生活北京师范大学出版社高二物理人教版》

【典例2】已知在$t_1$时刻简谐横波的波形如图2-6中实线所示,在$t_2$时刻该波的波形如图2-6中虚线所示,$t_2 - t_1 = 0.02s$.则：

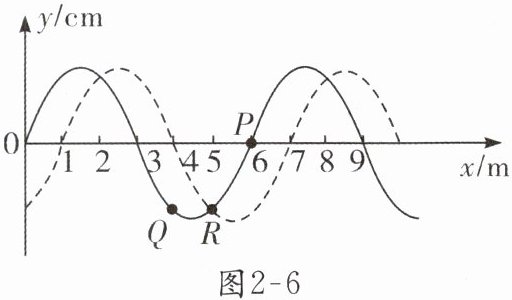
(1)求该波可能的传播速度；
(2)若已知$T ＜ t_2 - t_1 ＜ 2T$,且图中质点$P在t_1$时刻的瞬时速度方向向上,求波速；
(3)若$0.01s ＜ T ＜ 0.02s$,且从$t_1$时刻起,图中质点$Q比质点R$先回到平衡位置,求可能的波速.

答案： 【解析】：
(1)由图知波长$\lambda=6m$。波可能向右传播，也可能向左传播。
向右传播时，在$t_1\sim t_2$内波形向右匀速传播的距离为$x=(n+\frac{1}{6})\lambda$，$n=0,1,2,\cdots$，波速$v = \frac{x}{t_2 - t_1}=\frac{(n+\frac{1}{6})\lambda}{0.02s}=50(6n + 1)m/s$，$n=0,1,2,\cdots$。
向左传播时，在$t_1\sim t_2$内波形向左匀速传播的距离为$x=(n+\frac{5}{6})\lambda$，$n=0,1,2,\cdots$，波速$v = \frac{x}{t_2 - t_1}=\frac{(n+\frac{5}{6})\lambda}{0.02s}=50(6n + 5)m/s$，$n=0,1,2,\cdots$。
(2)已知$t_1$时刻质点$P$速度向上，根据“上下坡法”可知波向左传播。
又因为$T\lt t_2 - t_1\lt 2T$，即$T\lt 0.02s\lt 2T$，可得$0.01s\lt T\lt 0.02s$。
在这段时间内波向左传播的距离$x=(1+\frac{5}{6})\lambda=\frac{11}{6}\lambda$，波速$v = \frac{x}{t_2 - t_1}=\frac{\frac{11}{6}×6m}{0.02s}=550m/s$。
(3)已知$0.01s\lt T\lt 0.02s$，且从$t_1$时刻起，图中质点$Q$比质点$R$先回到平衡位置，说明$t_1$时刻质点$Q$速度方向向下，根据“上下坡法”可知波向右传播。
又因为$0.01s\lt T\lt 0.02s$，即$T\lt 0.02s\lt 2T$，在这段时间内波向右传播的距离$x=(1+\frac{1}{6})\lambda=\frac{7}{6}\lambda$，波速$v = \frac{x}{t_2 - t_1}=\frac{\frac{7}{6}×6m}{0.02s}=350m/s$。
【答案】：
(1)$v = 50(6n + 1)m/s$或$v = 50(6n + 5)m/s$，$n = 0,1,2,\cdots$
(2)$v = 550m/s$
(3)$v = 350m/s$

1.(多选)一单摆做简谐运动,在偏角增大的过程中,摆球的(AC).
A.位移增大
B.速度增大
C.回复力增大
D.机械能增大

答案： AC 解析:由简谐运动的特点可知,当偏角增大时,摆球偏离平衡位置的位移增大,故A正确;在偏角增大的过程中,动能转化为重力势能,所以速度减小,故B错误;由回复力F=-kx可知,位移增大,回复力增大,故C正确;单摆做简谐运动过程中只有重力做功,所以机械能守恒,故D错误.