2025年暑假生活北京师范大学出版社高二物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高二物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
4. (多选)如图 4 - 9,台秤上放一光滑平板,其左边固定一挡板,一轻质弹簧将挡板和一条形磁体连接起来,此时台秤读数为 $ F_1 $,现在磁体上方中心偏左位置固定一导体棒,当导体棒中通以方向如图的电流后,台秤读数为 $ F_2 $,则以下说法正确的是( )。
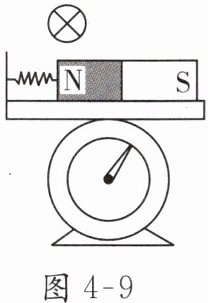
A.弹簧长度将变长
B.弹簧长度将变短
C.$ F_1 > F_2 $
D.$ F_1 < F_2 $

A.弹簧长度将变长
B.弹簧长度将变短
C.$ F_1 > F_2 $
D.$ F_1 < F_2 $
答案:
BC 解析:如答图4−1甲所示,导体棒处的磁场方向指向右上方,根据左手定则可知,导体棒受到的安培力方向垂直于磁场方向指向右下方,根据牛顿第三定律,对条形磁体受力分析,如答图4−1乙所示,所以F_N1>F_N2,即台秤示数F1>F2,C正确,D错误;在水平方向上,由于F'有向左的分力,磁体压缩弹簧,所以弹簧长度变短,B正确,A错误.
BC 解析:如答图4−1甲所示,导体棒处的磁场方向指向右上方,根据左手定则可知,导体棒受到的安培力方向垂直于磁场方向指向右下方,根据牛顿第三定律,对条形磁体受力分析,如答图4−1乙所示,所以F_N1>F_N2,即台秤示数F1>F2,C正确,D错误;在水平方向上,由于F'有向左的分力,磁体压缩弹簧,所以弹簧长度变短,B正确,A错误.

5. (多选)关于安培力和洛伦兹力,下列说法正确的是(
A.洛伦兹力和安培力是性质完全不同的两种力
B.安培力和洛伦兹力,其本质都是磁场对运动电荷的作用力
C.安培力和洛伦兹力,二者是等价的
D.安培力对通电导体能做功,但洛伦兹力对运动电荷不能做功
BD
)。A.洛伦兹力和安培力是性质完全不同的两种力
B.安培力和洛伦兹力,其本质都是磁场对运动电荷的作用力
C.安培力和洛伦兹力,二者是等价的
D.安培力对通电导体能做功,但洛伦兹力对运动电荷不能做功
答案:
BD 解析:安培力和洛伦兹力实际上都是磁场对运动电荷们作用力,但二者不是等价的,安培力实际上足洛伦兹力们宏观表现,它可以对通电导体做功,但洛伦兹力不能对运动电荷做功,B、D正确.
6. 如图 4 - 10,回旋加速器 $ D $ 形盒的半径为 $ R $,用来加速质量为 $ m $、电荷量为 $ q $ 的质子,质子每次经过电场区时,都恰好在电压为 $ U $ 时被加速,且电场可视为匀强电场,使质子由静止加速到能量为 $ E $ 后,由 $ A $ 孔射出。下列说法正确的是(
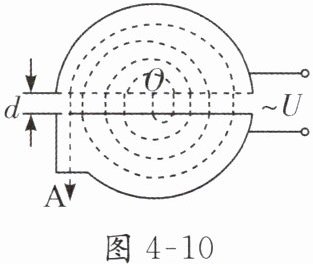
A.$ D $ 形盒半径 $ R $、磁感应强度 $ B $ 不变,加速电压 $ U $ 增大,质子在加速器中的运动时间将不变
B.$ D $ 形盒半径 $ R $、磁感应强度 $ B $ 不变,加速电压 $ U $ 越高,质子在加速器中的运动时间将越长
C.$ D $ 形盒半径 $ R $、磁感应强度 $ B $ 不变,加速电压 $ U $ 越高,质子飞出 $ D $ 形盒时的动能 $ E_k $ 将越大
D.磁感应强度 $ B $ 不变,加速电压 $ U $ 不变,$ D $ 形盒半径 $ R $ 越大、质子飞出 $ D $ 形盒时的动能 $ E_k $ 将越大
D
)。
A.$ D $ 形盒半径 $ R $、磁感应强度 $ B $ 不变,加速电压 $ U $ 增大,质子在加速器中的运动时间将不变
B.$ D $ 形盒半径 $ R $、磁感应强度 $ B $ 不变,加速电压 $ U $ 越高,质子在加速器中的运动时间将越长
C.$ D $ 形盒半径 $ R $、磁感应强度 $ B $ 不变,加速电压 $ U $ 越高,质子飞出 $ D $ 形盒时的动能 $ E_k $ 将越大
D.磁感应强度 $ B $ 不变,加速电压 $ U $ 不变,$ D $ 形盒半径 $ R $ 越大、质子飞出 $ D $ 形盒时的动能 $ E_k $ 将越大
答案:
D 解析:在回旋加速器中,每经过电场一次获得动能ΔE_k=qU,根据洛伦兹力提供向心力有$qvB=m\frac{v^2}{R},$当粒子们运动半径等于回旋加速器半径时粒子速度最大,动能最大$E_km=\frac{q^2B^2R^2}{2m}$无关,所以D形盒半径R、磁感应强度B不变,最大动能不变但是加速电压U越高每次获得动能增大,转的圈数减小而每圈的时间$T=\frac{2πm}{Bq}$是定值,所以加速时间将减小,A、B、C错误;根据$E_km=\frac{q^2B^2R^2}{2m}$可知,半径R越大,质子飞出D形盒时们动能E_k将越大,D正确.
7. 如图 4 - 11,两平行金属导轨间的距离 $ L = 0.4 m $,金属导轨所在的平面与水平面夹角 $ \theta = 37^{\circ} $,在导轨所在平面内分布着磁感应强度 $ B = 0.5 T $、方向垂直于导轨所在平面的匀强磁场。金属导轨的一端接有电动势 $ E = 4.5 V $、内阻 $ r = 0.5 \Omega $ 的直流电源。现把一个质量 $ m = 0.04 kg $ 的导体棒 $ ab $ 放在金属导轨上,导体棒恰好静止。导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻 $ R_0 = 2.5 \Omega $,金属导轨电阻不计,$ g $ 取 $ 10 m/s^2 $。已知 $ \sin 37^{\circ} = 0.6 $,$ \cos 37^{\circ} = 0.8 $,求:
(1) 通过导体棒的电流;
(2) 导体棒受到的安培力大小;
(3) 导体棒受到的摩擦力大小。
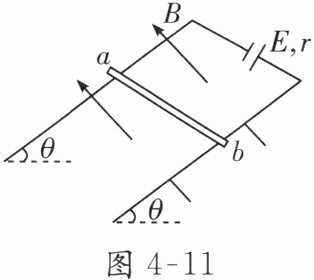
(1) 通过导体棒的电流;
(2) 导体棒受到的安培力大小;
(3) 导体棒受到的摩擦力大小。

答案:
解析:
(1)根据闭合电路欧姆定律$I=\frac{E}{R_0+r}=1.5A.(2)$导体棒受到的安培力F_安=BIL=0.lN.
(3)导体棒受力如答图4−2,将重力正交分解, $ F_1=mgsin37°=0.24N,$由于$F_1<F_$安,摩擦力F_f方向沿导轨向下,根据平衡条件有mgsin37°+F_f=F_安,解得F_f=0.06N.答案:
$ F_1=mgsin37°=0.24N,$由于$F_1<F_$安,摩擦力F_f方向沿导轨向下,根据平衡条件有mgsin37°+F_f=F_安,解得F_f=0.06N.答案:
(1)1.5A
(2)0.3N
(3)0.06N
解析:
(1)根据闭合电路欧姆定律$I=\frac{E}{R_0+r}=1.5A.(2)$导体棒受到的安培力F_安=BIL=0.lN.
(3)导体棒受力如答图4−2,将重力正交分解,
 $ F_1=mgsin37°=0.24N,$由于$F_1<F_$安,摩擦力F_f方向沿导轨向下,根据平衡条件有mgsin37°+F_f=F_安,解得F_f=0.06N.答案:
$ F_1=mgsin37°=0.24N,$由于$F_1<F_$安,摩擦力F_f方向沿导轨向下,根据平衡条件有mgsin37°+F_f=F_安,解得F_f=0.06N.答案:(1)1.5A
(2)0.3N
(3)0.06N
查看更多完整答案,请扫码查看


