《2025年暑假生活北京师范大学出版社高二物理人教版》

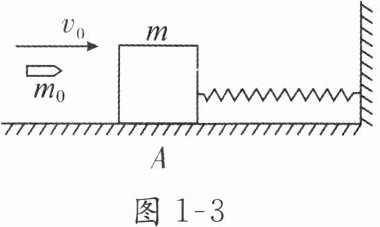
1. 如图 1 - 3 所示,质量为$m$的木块位于光滑水平地面上,木块与墙用水平轻弹簧连接,开始时木块静止在$A$位置. 现有一质量为$m_{0}的子弹以水平速度v_{0}$射向木块并嵌入其中,则当木块回到$A位置时的速度v的大小及此过程中墙对弹簧的冲量I$的大小分别为(B).


A.$\frac{m_{0}v_{0}}{m + m_{0}},0$
B.$\frac{m_{0}v_{0}}{m + m_{0}},2m_{0}v_{0}$
C.$\frac{m_{0}v_{0}}{m + m_{0}},\frac{2m_{0}^{2}v_{0}}{m + m_{0}}$
D.$\frac{m_{0}v_{0}}{m},2m_{0}v_{0}$

答案： B 解析:子弹射入木块过程,由于时间极短,子弹与木块间的内力远大于子弹和木块组成的系统受到的外力,以水平速度$v_{0}$的方向为正方向,由动量守恒定律得$m_{0}v_{0}=(m+m_{0})v'$,解得$v'=\frac{m_{0}v_{0}}{m+m_{0}}$;子弹和木块系统在弹簧弹力的作用下先做减速运动,后反向做加速运动,回到A位置时速度大小不变,即木块回到A位置时的速度大小$v=v'=\frac{m_{0}v_{0}}{m+m_{0}}$;子弹、木块和弹簧组成的系统受到的合力即墙对弹簧的作用力,根据动量定理得$I=-(m+m_{0})v-(m+m_{0})v'=-2m_{0}v_{0}$,所以墙对弹簧的冲量$I$的大小为$2m_{0}v_{0}$,故选B.

2. (多选)两个物体在光滑水平面上发生正碰,则可能出现的现象是(BCD).
A.质量大的物体动量变化大
B.两个物体动量变化大小相等,方向相反
C.一个物体的速度减小,另一个物体的速度增大
D.质量小的物体速度变化大

答案： BCD 解析:两个物体发生正碰,两物体组成的系统动量守恒,即$\Delta p=-\Delta p'$,两物体动量变化大小相等,方向相反,A错误,B正确;质量小的物体速度变化一定大,D正确;当发生碰撞的两个物体与原来同向运动时,碰后后面物体的速度减小,前面物体的速度增大,C正确.

3. (多选)动能相同的 A、B 两球($m_{A}＞m_{B}$)在光滑的水平面上相向运动,当两球相碰后,其中一球停止运动,则可判定ABD.
A.碰撞前 A 球的速度小于 B 球的速度
B.碰撞前 A 球的动量大于 B 球的动量
C.碰撞前后 A 球的动量变化量大于 B 球的动量变化量
D.碰撞后,A 球的速度一定为零,B 球朝反方向运动

答案： ABD 解析:A、B两球动能相同,且$m_{A}＞m_{B}$,可得$v_{B}＞v_{A}$,故A正确;再由动量和动能关系可得$p_{A}＞p_{B}$,故B正确;由动量守恒定律可知,碰撞前后A球的动量变化量大小等于B球的动量变化量大小,故C错误;碰撞后,A球的速度一定为零,B球朝反方向运动,故D正确.

4. 竖直发射的火箭质量为$6×10^{3}kg$,已知 1 s 喷出气体的质量为 200 kg. 若要使火箭获得$20.2m/s^{2}$的向上的加速度,则喷出气体的速度大小应为(不考虑喷出气体对火箭质量的影响)(C).
A.700 m/s
B.800 m/s
C.900 m/s
D.1 000 m/s

答案： C 解析:火箭和喷出的气体动量守恒,即1s内喷出气体的动量等于火箭1s内增加的动量,即$m_{\text{气}}v_{\text{气}}=m_{\text{箭}}\Delta v_{\text{箭}}$,由动量定理得火箭获得的动力$F=\frac{m_{\text{箭}}\Delta v_{\text{箭}}}{t}=\frac{m_{\text{气}}v_{\text{气}}}{t}=200v_{\text{气}}$,又$F-m_{\text{箭}}g=m_{\text{箭}}a$,得$v_{\text{气}}=900\ \text{m/s}$.

5. (多选)如图 1 - 4 所示,一平台到地面的高度$h = 0.45m$,质量$m' = 0.3kg$的木块放在平台的右端,木块与平台间的动摩擦因数为$\mu = 0.2$. 地面上有一质量$m = 0.1kg$的玩具青蛙,到平台右侧的水平距离$x = 1.2m$,旋紧发条后释放,让玩具青蛙斜向上跳起,当玩具青蛙到达木块的位置时速度恰好沿水平方向,玩具青蛙立即抱住木块并和木块一起滑行. 已知木块和玩具青蛙均可视为质点,玩具青蛙抱住木块过程时间极短,空气阻力不计,重力加速度$g取10m/s^{2}$,则下列说法正确的是AD.
A.玩具青蛙在空中运动的时间为 0.3 s
B.玩具青蛙在平台上运动的时间为 2 s
C.玩具青蛙起跳时的速度大小为 3 m/s
D.木块开始滑动时的速度大小为 1 m/s

答案： AD 解析:由$h=\frac{1}{2}gt_{1}^{2}$得玩具青蛙在空中运动的时间$t_{1}=0.3\ \text{s}$,A正确;玩具青蛙离开地面时的水平速度和竖直速度分别为$v_{x}=\frac{x}{t_{1}}=4\ \text{m/s}$,$v_{y}=gt_{1}=3\ \text{m/s}$,则玩具青蛙起跳时的速度大小为$v_{0}=\sqrt{v_{x}^{2}+v_{y}^{2}}=5\ \text{m/s}$,C错误;木块和玩具青蛙组成的系统在水平方向上动量守恒,以水平向左为正方向,由动量守恒定律得$mv_{x}=(m'+m)v$,解得木块开始滑动时的速度大小为$v=1\ \text{m/s}$,D正确;对木块及玩具青蛙系统,由动量定理得$-\mu(m'+m)gt_{2}=0-(m'+m)v$,解得玩具青蛙在平台上运动的时间为$t_{2}=0.5\ \text{s}$,B错误.

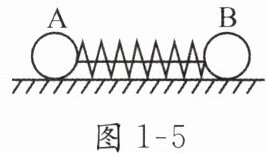
6. 如图 1 - 5 所示,光滑水平面上有大小相同的 A、B 两球,两球质量关系为$m_{B}= 2m_{A}$,A、B 两球间有一被压缩的弹簧,弹簧被细线锁定. 现烧断细线解除锁定,弹簧弹开小球,B 球获得的动量大小为$10kg\cdot m/s$,规定向右为正方向,则(C).

A.A 球受到的冲量为$10kg\cdot m/s$
B.A 球获得的动量大小为$5kg\cdot m/s$
C.弹开后 A、B 两球速度大小之比为$2:1$
D.弹开后 A、B 两球速度大小之比为$1:2$

答案： C 解析:根据动量守恒定律可知弹簧弹开之前A、B组成的系统总动量为零,弹开后B球获得的动量大小为$10\ \text{kg}\cdot\text{m/s}$,则A球获得大小相等、方向相反的动量$-10\ \text{kg}\cdot\text{m/s}$;再根据动量定理可知A球受到的冲量等于A球的动量变化量,即$(-10\ \text{kg}\cdot\text{m/s})-0=-10\ \text{kg}\cdot\text{m/s}$,故A、B错误.弹开后,因为A、B两球的动量大小总是相等,速度之比等于质量的反比,即$2:1$,故C正确,D错误.