2025年暑假作业明天出版社高一物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业明天出版社高一物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 某长跑运动员在一次野外训练中,出发地和目的地的直线距离为8km,从出发地到目的地用了30min,运动轨迹的长度为10km。下列说法正确的是(
A.在整个过程中运动员运动的位移大小是8km
B.在整个过程中运动员通过的路程是8km
C.在整个过程中运动员的平均速度是20km/h
D.在整个过程中运动员的平均速度是16km/h
AD
)A.在整个过程中运动员运动的位移大小是8km
B.在整个过程中运动员通过的路程是8km
C.在整个过程中运动员的平均速度是20km/h
D.在整个过程中运动员的平均速度是16km/h
答案:
AD 出发地和目的地之间的直线距离为整个运动过程的位移大小,路程等于运动轨迹的长度,平均速度$\overline{v}=\frac{x}{t}=\frac{8\ \text{km}}{\frac{1}{2}\ \text{h}}=16\ \text{km/h}$,选项A、D正确,B、C错误。
9. 如图是用打点计时器测小车瞬时速度时得到的一条纸带的一部分,从0点开始按照打点的先后依次标为0,1,2,3,4,5,6,…,现在量得0、1间的距离$x_1= 5.18cm,1、$2间的距离$x_2= 4.40cm,2、$3间的距离$x_3= 3.62cm,3、$4间的距离$x_4= 2.78cm,4、$5间的距离$x_5= 2.00cm,5、$6间的距离$x_6= 1.22cm($每0.02s打一次点)。

(1)在实验中,使用打点计时器时应先______再______(选填“释放纸带”或“启动电源”)。
(2)根据上面的记录,计算打点计时器在打1、2、3、4、5点时小车的速度值并填在表中。
|位置|1|2|3|4|5|
|$v/(m·s⁻^1)$| | | | | |
(3)根据(2)中表格中的数据,在图中画出小车的速度—时间图像,并说明小车速度变化的特点。

(1)在实验中,使用打点计时器时应先______再______(选填“释放纸带”或“启动电源”)。
(2)根据上面的记录,计算打点计时器在打1、2、3、4、5点时小车的速度值并填在表中。
|位置|1|2|3|4|5|
|$v/(m·s⁻^1)$| | | | | |
(3)根据(2)中表格中的数据,在图中画出小车的速度—时间图像,并说明小车速度变化的特点。

答案:
解析:
(2)某点的瞬时速度可用包含该点的一段位移内的平均速度表示,打相邻两计数点的时间间隔$\Delta t = 2×0.02\ \text{s}=0.04\ \text{s}$,则打1点时:$v_{1}=\frac{x_{1}+x_{2}}{2\Delta t}\approx1.20\ \text{m/s}$ 打2点时:$v_{2}=\frac{x_{2}+x_{3}}{2\Delta t}\approx1.00\ \text{m/s}$ 打3点时:$v_{3}=\frac{x_{3}+x_{4}}{2\Delta t}=0.80\ \text{m/s}$ 打4点时:$v_{4}=\frac{x_{4}+x_{5}}{2\Delta t}\approx0.60\ \text{m/s}$ 打5点时:$v_{5}=\frac{x_{5}+x_{6}}{2\Delta t}\approx0.40\ \text{m/s}$ 将数值填入表格中:

(3)描点并连线得小车的速度—时间图像,如图所示,由图像可知,小车速度逐渐减小。
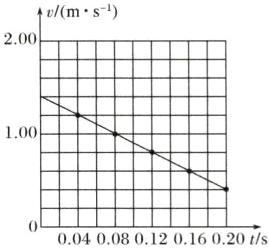
答案:
(1)启动电源 释放纸带
(2)、
(3)见解析
解析:
(2)某点的瞬时速度可用包含该点的一段位移内的平均速度表示,打相邻两计数点的时间间隔$\Delta t = 2×0.02\ \text{s}=0.04\ \text{s}$,则打1点时:$v_{1}=\frac{x_{1}+x_{2}}{2\Delta t}\approx1.20\ \text{m/s}$ 打2点时:$v_{2}=\frac{x_{2}+x_{3}}{2\Delta t}\approx1.00\ \text{m/s}$ 打3点时:$v_{3}=\frac{x_{3}+x_{4}}{2\Delta t}=0.80\ \text{m/s}$ 打4点时:$v_{4}=\frac{x_{4}+x_{5}}{2\Delta t}\approx0.60\ \text{m/s}$ 打5点时:$v_{5}=\frac{x_{5}+x_{6}}{2\Delta t}\approx0.40\ \text{m/s}$ 将数值填入表格中:

(3)描点并连线得小车的速度—时间图像,如图所示,由图像可知,小车速度逐渐减小。

答案:
(1)启动电源 释放纸带
(2)、
(3)见解析
10. 有些国家的交通管理部门为了交通安全,特别制定了死亡加速度为500g(g取$10m/s^2),$以醒世人,意思是如果行车加速度超过此值,将有生命危险。那么大的加速度,一般情况下车辆是达不到的,但如果发生交通事故时,有可能达到这一数值。试问:
(1)一辆以54km/h的速度行驶的货车与一辆以36km/h的速度行驶的摩托车相向而行发生碰撞,摩托车驾驶员以与碰撞前货车的速度被撞飞,碰撞时间为$2.5×10⁻^3s,$摩托车驾驶员是否有生命危险?
(2)为了防止碰撞,两车的驾驶员同时紧急刹车,货车、摩托车急刹车后到完全静止所需时间分别为3s、2s,货车的加速度与摩托车的加速度大小之比为多少?
(1)一辆以54km/h的速度行驶的货车与一辆以36km/h的速度行驶的摩托车相向而行发生碰撞,摩托车驾驶员以与碰撞前货车的速度被撞飞,碰撞时间为$2.5×10⁻^3s,$摩托车驾驶员是否有生命危险?
(2)为了防止碰撞,两车的驾驶员同时紧急刹车,货车、摩托车急刹车后到完全静止所需时间分别为3s、2s,货车的加速度与摩托车的加速度大小之比为多少?
答案:
解析:
(1)已知$v_{1}=54\ \text{km/h}=15\ \text{m/s}$,$v_{2}=36\ \text{km/h}=10\ \text{m/s}$。两车碰撞过程中,取摩托车的初速度方向为正方向,摩托车的速度变化量$\Delta v = v_{2}-v_{1}=-15\ \text{m/s}-10\ \text{m/s}=-25\ \text{m/s}$,两车相碰撞时摩托车驾驶员的加速度大小为$a=\left|\frac{\Delta v}{\Delta t}\right|=\frac{25\ \text{m/s}}{2.5×10^{-3}\ \text{s}}=10000\ \text{m/s}^{2}=1000g$,$1000g>500g$,因此摩托车驾驶员有生命危险。
(2)设货车、摩托车的加速度大小分别为$a_{1}$、$a_{2}$,根据加速度定义得$\frac{a_{1}}{a_{2}}=\frac{\frac{|\Delta v_{1}|}{\Delta t_{1}}}{\frac{|\Delta v_{2}|}{\Delta t_{2}}}=\frac{\frac{15}{3}\ \text{m/s}^{2}}{\frac{10}{2}\ \text{m/s}^{2}}=\frac{1}{1}$。
答案:
(1)有生命危险
(2)$1:1$
(1)已知$v_{1}=54\ \text{km/h}=15\ \text{m/s}$,$v_{2}=36\ \text{km/h}=10\ \text{m/s}$。两车碰撞过程中,取摩托车的初速度方向为正方向,摩托车的速度变化量$\Delta v = v_{2}-v_{1}=-15\ \text{m/s}-10\ \text{m/s}=-25\ \text{m/s}$,两车相碰撞时摩托车驾驶员的加速度大小为$a=\left|\frac{\Delta v}{\Delta t}\right|=\frac{25\ \text{m/s}}{2.5×10^{-3}\ \text{s}}=10000\ \text{m/s}^{2}=1000g$,$1000g>500g$,因此摩托车驾驶员有生命危险。
(2)设货车、摩托车的加速度大小分别为$a_{1}$、$a_{2}$,根据加速度定义得$\frac{a_{1}}{a_{2}}=\frac{\frac{|\Delta v_{1}|}{\Delta t_{1}}}{\frac{|\Delta v_{2}|}{\Delta t_{2}}}=\frac{\frac{15}{3}\ \text{m/s}^{2}}{\frac{10}{2}\ \text{m/s}^{2}}=\frac{1}{1}$。
答案:
(1)有生命危险
(2)$1:1$
查看更多完整答案,请扫码查看


