2025年暑假作业明天出版社高一物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业明天出版社高一物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 在“金星凌日”的精彩天象中,观察到太阳表面上有颗小黑点缓慢“走过”,持续时间达六个半小时,那便是金星,如图所示,下面说法正确的是(
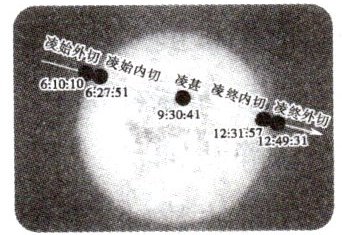
A.地球在金星与太阳之间
B.观测“金星凌日”时可将太阳看成质点
C.以太阳为参考系,地球是运动的
D.以太阳为参考系,金星是运动的
CD
)
A.地球在金星与太阳之间
B.观测“金星凌日”时可将太阳看成质点
C.以太阳为参考系,地球是运动的
D.以太阳为参考系,金星是运动的
答案:
CD
8. 如图所示为甲、乙两物体相对于同一参考系的$ x - t $图像。下列说法正确的是(
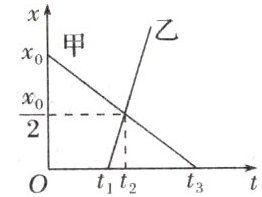
A.甲、乙两物体的出发点相距$ x_{0} $
B.甲物体比乙物体早出发的时间为$ t_{1} $
C.甲、乙两物体同向运动
D.甲、乙两物体在$ t_{2} $时刻相遇
ABD
)
A.甲、乙两物体的出发点相距$ x_{0} $
B.甲物体比乙物体早出发的时间为$ t_{1} $
C.甲、乙两物体同向运动
D.甲、乙两物体在$ t_{2} $时刻相遇
答案:
ABD 甲物体在t=0时刻出发,其运动方向与规定的正方向相反,出发点距原点的距离为x₀。乙物体在t=t₁时刻从原点出发,其运动方向沿规定的正方向,两物体运动方向相反。故A、B正确,C错误。甲、乙两物体在t₂时刻处于同一位置,即相遇,故D正确。
9. 如图所示,运动场的直线跑道上,每隔4m放一空瓶。运动员进行往返跑训练时,推倒中间O点处的空瓶后,跑向O点右侧距O最近的A点,将空瓶推倒后返回,再推倒O点左侧$ A' $点处的空瓶,之后再跑向右侧的B点,将空瓶推倒,再向左,如此反复。取向右为正方向,下表是运动员在不同时刻对应的位置坐标。

|时刻$ t/s $|0|2|6|12|20|30|
|位置坐标$ x/m $|0|4|-4|8|-8|12|
由表格中所给数据试求:
(1)0~2s内运动员的位移;
(2)2~6s内运动员的位移;
(3)前20s内运动员的路程和位移。

|时刻$ t/s $|0|2|6|12|20|30|
|位置坐标$ x/m $|0|4|-4|8|-8|12|
由表格中所给数据试求:
(1)0~2s内运动员的位移;
(2)2~6s内运动员的位移;
(3)前20s内运动员的路程和位移。
答案:
解析:
(1)由坐标求位移时,位移Δx=x₂-x₁,故0~2 s内运动员的位移Δx₁=4 m-0=4 m,方向向右。
(2)2~6 s内运动员的位移Δx₂=-4 m-4 m=-8 m,负号表示方向向左。
(3)画出运动员在前20 s内的运动示意图,如图所示,则前20 s内的路程s=OA+AA'+A'B+BB'=40 m,位移Δx₃=-8 m-0=-8 m,负号表示方向向左。

答案:
(1)大小为4 m,方向向右
(2)大小为8 m,方向向左
(3)40 m 大小为8 m,方向向左
解析:
(1)由坐标求位移时,位移Δx=x₂-x₁,故0~2 s内运动员的位移Δx₁=4 m-0=4 m,方向向右。
(2)2~6 s内运动员的位移Δx₂=-4 m-4 m=-8 m,负号表示方向向左。
(3)画出运动员在前20 s内的运动示意图,如图所示,则前20 s内的路程s=OA+AA'+A'B+BB'=40 m,位移Δx₃=-8 m-0=-8 m,负号表示方向向左。

答案:
(1)大小为4 m,方向向右
(2)大小为8 m,方向向左
(3)40 m 大小为8 m,方向向左
10. 一位电脑动画爱好者设计了一个“猫捉老鼠”的动画,如图所示,在一个棱长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口在木箱的另一顶点A处。若老鼠仅沿着棱边奔跑,聪明的猫选择了一条最短的路线奔向洞口,结果猫在洞口A再次捉到了老鼠。从老鼠逃出到再次被捉,问:

(1)老鼠的位移大小及最短路程是多少?
(2)猫的位移大小和路程是多少?

(1)老鼠的位移大小及最短路程是多少?
(2)猫的位移大小和路程是多少?
答案:
解析:
(1)由几何关系可知,老鼠从顶点G出发,走过的最短路程为3a(三条棱),位移大小为$3a$。
(2)将立体图形展开,如图所示,当猫按照GA线走时,路程最短,则最短路程为$\sqrt{ (a²+(2a)²)}=\sqrt 5a$,猫的位移大小也是√3a。

答案:
(1)$\sqrt 3a$ 3a
(2)$\sqrt 3a$ $\sqrt 5a$
解析:
(1)由几何关系可知,老鼠从顶点G出发,走过的最短路程为3a(三条棱),位移大小为$3a$。
(2)将立体图形展开,如图所示,当猫按照GA线走时,路程最短,则最短路程为$\sqrt{ (a²+(2a)²)}=\sqrt 5a$,猫的位移大小也是√3a。

答案:
(1)$\sqrt 3a$ 3a
(2)$\sqrt 3a$ $\sqrt 5a$
查看更多完整答案,请扫码查看


