《2025年暑假作业明天出版社高一物理》

7. 两个半径、材料完全相同的金属小球,所带电荷量之比为$1:7$,间距为r,把两球相互接触后再放回原来的位置上,则相互作用力可能为原来的(BCD)
A.$\frac {7}{16}$
B.$\frac {7}{9}$
C.$\frac {9}{7}$
D.$\frac {16}{7}$

答案： BCD

8. A、B是一条电场线上的两个点,一带负电的微粒仅在电场力作用下以一定初速度从A点沿电场线运动到B点,其速度—时间图像如图所示。则这一电场不可能是下列图中的(BCD)

答案： BCD 负电荷受力方向和电场线方向相反,由v-t图像可知,微粒做加速度不断增大的减速运动,电场力逐渐变大、且与运动方向相反,故A可能,B、C、D不可能。故B、C、D正确。

9. 如图所示,电荷量$Q= 2×10^{-7}C$的正点电荷A固定在空间中O点,将质量为$m= 2×10^{-4}kg$、电荷量$q= 1×10^{-7}C$的另一正点电荷B从O点正上方0.5m的某处由静止释放,B运动过程中速度最大位置在P点。静电力常量$k= 9×10^{9}N\cdot m^{2}/C^{2}$,重力加速度g取$10m/s^{2}$。求：

(1)B释放时的加速度大小；
(2)P、O间的距离L。

答案： 解析:
(1)根据牛顿第二定律有$mg-k\frac{qQ}{L^2}=ma$解得$a=6.4\ \text{m/s}^2$。
(2)当B受到合力为零时,速度最大,则P、O间的距离L满足$mg=k\frac{qQ}{L^2}$解得$L=0.3\ \text{m}$。答案:
(1)$6.4\ \text{m/s}^2$
(2)$0.3\ \text{m}$

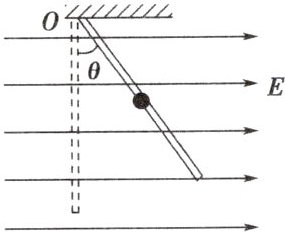
10. 如图所示,长为$L= 0.12m$的绝缘轻杆上端固定在O点,质量为$m= 0.6kg$、电荷量为$q= +0.5C$的金属小球套在绝缘轻杆上,空间存在水平向右的匀强电场,球与杆间的动摩擦因数为$\mu =0.75$。当杆竖直固定放置时,小球恰好能匀速下滑,g取$10m/s^{2}$。

(1)求匀强电场的电场强度大小；
(2)改变轻杆与竖直方向的夹角,使小球下滑过程中与杆之间的摩擦力为0,并将小球从O点由静止释放,求小球离开杆时的速度大小。

答案： 解析:
(1)当杆竖直固定放置时,有$F_N=Eq,mg=F_f,F_f=\mu F_N$,联立解得$E=\frac{mg}{\mu q}$,代入数据得$E=16\ \text{N/C}$。
(2)小球与杆之间的摩擦力为0,说明小球与杆之间的弹力为0,则有$Eq\cos\theta=mg\sin\theta$,联立解得$\tan\theta=\frac{Eq}{mg}$,代入数据得$\tan\theta=\frac{4}{3}$,则可得$\theta=53^\circ$。设小球的加速度为a,则有$mg\cos53^\circ+Eq\sin53^\circ=ma$,代入数据解得$a=\frac{50}{3}\ \text{m/s}^2$。由运动学规律有$v^2=2aL$,代入数据解得小球离开杆时的速度$v=2\ \text{m/s}$。答案:
(1)$16\ \text{N/C}$
(2)$2\ \text{m/s}$