《2025年暑假作业甘肃少年儿童出版社五年级数学人教版》

一、按要求在下面的圈里填数。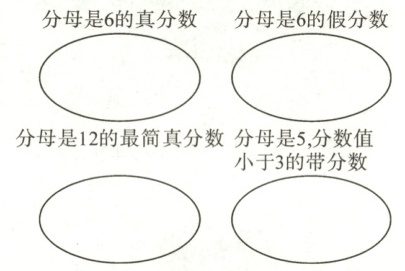

答案： 【解析】：
真分数是指分子小于分母的分数。已知分母是6，那么分子要小于6，所以分母是6的真分数有$\frac{1}{6}$、$\frac{2}{6}$、$\frac{3}{6}$、$\frac{4}{6}$、$\frac{5}{6}$。
最简分数是指分子、分母只有公因数1的分数。分母是12，分子要小于12且与12只有公因数1，所以分母是12的最简真分数有$\frac{1}{12}$、$\frac{5}{12}$、$\frac{7}{12}$、$\frac{11}{12}$。
假分数是指分子大于或者等于分母的分数。分母是6，那么分子要大于或等于6，所以分母是6的假分数有无数个，这里可填$\frac{6}{6}$、$\frac{7}{6}$、$\frac{8}{6}$等。
带分数是由整数和真分数合成的数。分母是5，分数值小于3，那么整数部分可以是0、1、2。当整数部分是0时，分数部分可以是$\frac{1}{5}$、$\frac{2}{5}$、$\frac{3}{5}$、$\frac{4}{5}$；当整数部分是1时，分数部分可以是$\frac{1}{5}$、$\frac{2}{5}$、$\frac{3}{5}$、$\frac{4}{5}$；当整数部分是2时，分数部分可以是$\frac{1}{5}$、$\frac{2}{5}$、$\frac{3}{5}$、$\frac{4}{5}$，所以分母是5，分数值小于3的带分数有$1\frac{1}{5}$、$1\frac{2}{5}$、$2\frac{1}{5}$等。
【答案】：
分母是6的真分数：$\frac{1}{6}$，$\frac{2}{6}$，$\frac{3}{6}$，$\frac{4}{6}$，$\frac{5}{6}$；
分母是6的假分数：$\frac{6}{6}$，$\frac{7}{6}$，$\frac{8}{6}$；
分母是12的最简真分数：$\frac{1}{12}$，$\frac{5}{12}$，$\frac{7}{12}$，$\frac{11}{12}$；
分母是5，分数值小于3的带分数：$1\frac{1}{5}$，$1\frac{2}{5}$，$2\frac{1}{5}$。

二、把下面的分数从小到大排列起来。
$\frac {2}{7}$、$\frac {5}{7}和\frac {2}{9}$
$3\frac {2}{5}$、$3\frac {2}{7}和3\frac {2}{9}$

答案： 【解析】：对于第一组分数$\frac{2}{7}$、$\frac{5}{7}$和$\frac{2}{9}$，先比较同分母的$\frac{2}{7}$和$\frac{5}{7}$，分母相同，分子越大分数越大，所以$\frac{2}{7} ＜ \frac{5}{7}$；再比较分子相同的$\frac{2}{7}$和$\frac{2}{9}$，分子相同，分母越大分数越小，所以$\frac{2}{9} ＜ \frac{2}{7}$，综上可得$\frac{2}{9} ＜ \frac{2}{7} ＜ \frac{5}{7}$。
对于第二组带分数$3\frac{2}{5}$、$3\frac{2}{7}$和$3\frac{2}{9}$，整数部分相同，只需比较分数部分。分数部分分子相同都是2，分母越大分数越小，所以$\frac{2}{9} ＜ \frac{2}{7} ＜ \frac{2}{5}$，因此带分数的大小顺序为$3\frac{2}{9} ＜ 3\frac{2}{7} ＜ 3\frac{2}{5}$。
【答案】：$\frac{2}{9} ＜ \frac{2}{7} ＜ \frac{5}{7}$；$3\frac{2}{9} ＜ 3\frac{2}{7} ＜ 3\frac{2}{5}$

三、一个长方形的周长为2分米,宽为$\frac {1}{4}$分米,长是多少分米？

答案： 【解析】：
设长方形的长为$L$分米，宽为$W$分米。根据题意，周长$P = 2$分米，宽$W = \frac{1}{4}$分米。
长方形的周长公式为：
$P = 2(L + W)$
将已知值代入公式：
$2 = 2(L + \frac{1}{4})$
解这个方程：
$2 = 2L + \frac{1}{2}$
$2 - \frac{1}{2} = 2L$
$\frac{3}{2} = 2L$
$L = \frac{3}{4}$
【答案】：$\frac{3}{4}$分米

1. $25÷0.5= 50$可以说25能被0.5(B)
A.整除
B.除尽

答案： 【解析】：
整除的概念通常用于整数之间，即一个整数能够被另一个整数整除，意味着除法的结果是整数且没有余数。然而，在本题中，25和0.5都不是整数，尽管25除以0.5的结果是整数50，但我们一般不说25能被0.5整除。
除尽则是一个更宽泛的概念，它只要求除法的结果是一个确定的数，不限制这个数必须是整数。因此，25除以0.5等于50，我们可以说25能被0.5除尽。
【答案】：B

2. 8是32和48的(B)
A.因数
B.公因数
C.最大公因数

答案： 【解析】：
首先，我们来看选项A：因数。因数是指能够整除给定数的数。8能够整除32和48，所以8是32和48的因数，这个选项本身是正确的，但题目问的是8与32和48的更具体的关系。
接着，我们看选项B：公因数。公因数是指两个或多个数共有的因数。8既是32的因数也是48的因数，所以8是32和48的公因数。
最后，我们看选项C：最大公因数。最大公因数是指两个或多个数的所有公因数中最大的一个。为了判断8是否是32和48的最大公因数，我们需要找出32和48的所有公因数，并从中找出最大的一个。32的因数有1, 2, 4, 8, 16, 32；48的因数有1, 2, 3, 4, 6, 8, 12, 16, 24, 48。它们共同的因数有1, 2, 4, 8, 16，其中最大的是16，所以8不是32和48的最大公因数。
综上所述，8是32和48的公因数，但不是最大公因数。
【答案】：B

3. 8和9是(C)
A.质数
B.合数
C.互质数

答案： 【解析】：
质数：一个大于1的自然数，除了1和它本身以外不再有其他因数。
合数：一个大于1的自然数，除了1和它本身以外还有其他因数。
互质数：两个或多个整数共有的唯一正因数只有1的数。
8的因数有：1, 2, 4, 8。
9的因数有：1, 3, 9。
8和9除了1以外，没有其他共同的因数，但它们各自除了1和本身外还有其他因数，所以它们不是质数，但满足互质数的定义中的“共有的唯一正因数只有1”这一条件在两者之间（尽管这个定义通常用于描述多个数之间的关系，而这里我们是在判断两个数是否互质）。然而，根据题目选项，我们需要判断它们是否单独是质数或合数，或者它们作为一对数是否是互质数。
A. 8和9都不是质数，因为它们都有除了1和本身以外的因数。
B. 8和9都是合数，但这并不是题目询问的，题目询问的是它们之间的关系。
C. 8和9是互质数，因为它们只有1这个公因数。
【答案】：C

五、一个最简分数加上它的一个分数单位是1,减去它的一个分数单位是$\frac {7}{8}$。这个最简分数是多少？(方法提示：根据第一个条件,可知这个最简分数的分母比分子多1)

答案： 解：设这个最简分数的分子为$x$，因为分母比分子多$1$，所以分母为$x + 1$，则这个分数为$\frac{x}{x + 1}$。
由题意得：$\frac{x}{x + 1} - \frac{1}{x + 1} = \frac{7}{8}$
即：$\frac{x - 1}{x + 1} = \frac{7}{8}$
交叉相乘：$8(x - 1) = 7(x + 1)$
$8x - 8 = 7x + 7$
$8x - 7x = 7 + 8$
$x = 15$
分母为：$15 + 1 = 16$
所以这个最简分数是$\frac{15}{16}$。
答：这个最简分数是$\frac{15}{16}$。

六、在$\frac {6}{12-4x}$中,当x为多少时,分数无意义？

答案： 要使分数$\frac{6}{12 - 4x}$无意义，则分母为$0$，即：
$12 - 4x = 0$
$-4x = -12$
$x = 3$
答：当$x = 3$时，分数无意义。

七、在$\frac {3-2x}{5}$中,当x为多少时,分数值为0？当x为多少时是分数单位？

答案： 解：要使分数值为0，则分子为0，分母不为0。
$3 - 2x = 0$
$2x = 3$
$x = \frac{3}{2}$
分数单位是指分子为1的分数。
$\frac{3 - 2x}{5} = \frac{1}{5}$
$3 - 2x = 1$
$2x = 2$
$x = 1$
当$x = \frac{3}{2}$时，分数值为0；当$x = 1$时是分数单位。