《2025年暑假作业甘肃少年儿童出版社五年级数学人教版》

一、下面图案分别是由哪个图形经过什么变化得到的？

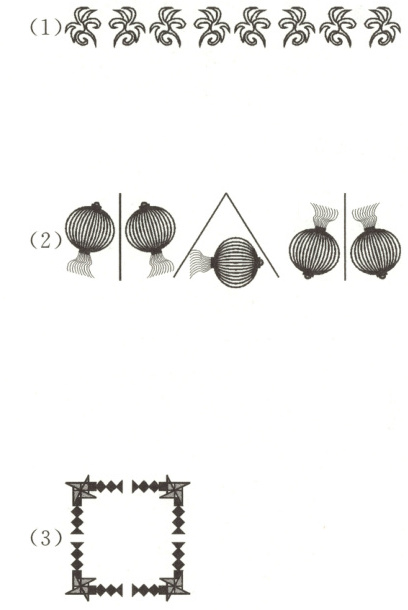
答案： 1. 对于（1）：
答案：是由一个基本图形经过平移得到的。
2. 对于（2）：
答案：是由一个基本图形经过旋转和平移得到的（先旋转再平移等多种组合方式，答案不唯一）。
3. 对于（3）：
答案：是由一个基本图形经过旋转和平移得到的（先旋转再平移等多种组合方式，答案不唯一）。

二、看图回答下面的问题。

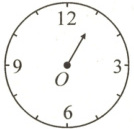
1. 指针从“12”绕O点旋转到“1”,指针旋转了(30)度。
2. 指针从“1”绕O点顺时针旋转90°到了(4)。
3. 指针从“3”绕O点顺时针转到了“10”,旋转了(210)度。

答案： 1. 30
2. 4
3. 210

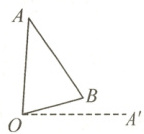
三、将下图中三角形AOB绕O点顺时针旋转90°。

答案： 【解析】：
在旋转时，O点位置保持不变，A点绕O点顺时针旋转90°到达A'的位置，B点绕O点顺时针旋转90°到达B'的位置。
确定旋转后的新坐标或位置关系，A'在O点右侧水平距离与原来A到O的垂直距离相同，B'在O点下方水平距离与原来B到O的水平距离相同。
连接O、A'和O、B'，得到旋转后的图形△A'OB'。
【答案】：在图上作出三角形$A^{\prime}OB^{\prime}$，其中$A^{\prime}$在O点右方，$B^{\prime}$在O点下方，且$OA^{\prime}\perp OA$，$OB^{\prime}\perp OB$，$\angle A'OB'=90^\circ$。

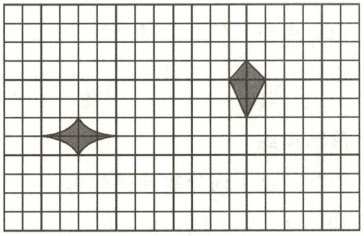
四、利用旋转设计美丽的图案。

答案： 【解析】：
本题是利用图形的旋转来设计图案，关键在于确定旋转中心、旋转方向和旋转角度。
观察给定图形，可选取图形的某个特殊点（如菱形的顶点等）作为旋转中心，一般选择图形的中心或对称点等位置较为合适。
旋转方向可以是顺时针或逆时针，旋转角度常见的有$90^{\circ}$、$180^{\circ}$、$270^{\circ}$等。
以左下角菱形的右下顶点为旋转中心，将菱形顺时针旋转$90^{\circ}$，得到一个新的菱形位置；再以同样的旋转中心，继续顺时针旋转$90^{\circ}$，又得到一个位置；再旋转$90^{\circ}$完成一圈。对于右上角的菱形也采用类似的操作，通过不断旋转可以得到更多重复的图形，从而组合成美丽的图案。
【答案】：以菱形的某个顶点为旋转中心，顺时针或逆时针旋转$90^{\circ}$（或其他合适角度如$180^{\circ}$、$270^{\circ}$等），多次旋转后组合成图案。