《2025年小学生学习指导丛书四年级数学上册人教版》

1. 杨明在游泳池的 $ A $ 处游泳,现在他想尽快游上岸,你能帮他设计一条最近的路线吗？请在下图中画出来。

答案： 从$A$点垂直向上岸边画一条直线（用直尺画出，并标记垂足为上岸点），这条垂线段就是杨明尽快游上岸的最近路线。

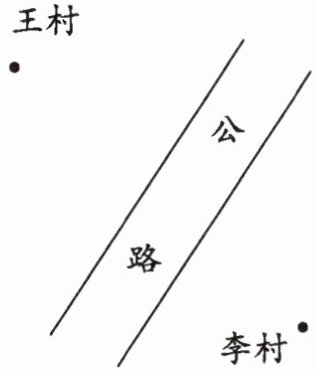
2. 王村和李村各修一条水泥路通到公路,怎么修最合理？试着画一画。

答案： 本题可根据“点到直线的距离中，垂线段最短”这一原理来确定修路的合理路线。
从王村和李村分别向公路作垂线段，沿垂线段修路最合理。
画图步骤：使用三角板的直角，将三角板的一条直角边与公路重合，移动三角板使另一条直角边分别经过王村和李村，沿着经过王村和李村的直角边分别画直线，与公路相交，这两条垂线段就是应该修的路。
结论：从王村和李村向公路作的垂线段就是最合理的修路路线。

3. 王奶奶沿着河边围了一块梯形菜地(菜地的一边靠着河岸且河岸足够长),菜地的上底长 $ 6 $ 米,下底长 $ 11 $ 米,两腰各是 $ 8 $ 米,她共用了 $ 22 $ 米长的篱笆。你知道她是怎么围的吗？请画一画。

答案： 本题可通过计算梯形周长与已用篱笆长度的关系，结合梯形一边靠河岸的条件来确定围法。
梯形的周长为上底、下底与两腰长度之和，该梯形菜地上底$6$米、下底$11$米、两腰各$8$米，其周长为$6 + 11 + 8 + 8 = 33$米。
因为河岸足够长，菜地一边靠河岸，所以靠河岸的那边不需要篱笆。
已知共用$22$米长的篱笆，$33 - 22 = 11$米，而梯形下底正好是$11$米，所以是把下底靠着河岸围的。
画图：可简单画出梯形，在下方（下底）标注靠着河岸（波浪线表示河岸）。

4. 右图中,直线 $ a $ 与直线 $ b $ 互相垂直吗？请说明理由。

答案： 解：直线$a$与直线$b$互相垂直。
理由：因为$180^{\circ}-55^{\circ}-35^{\circ}=90^{\circ}$，即直线$a$与直线$b$相交所成的角为$90^{\circ}$，根据垂直的定义：如果两条直线相交成直角，就说这两条直线互相垂直，所以直线$a$与直线$b$互相垂直。

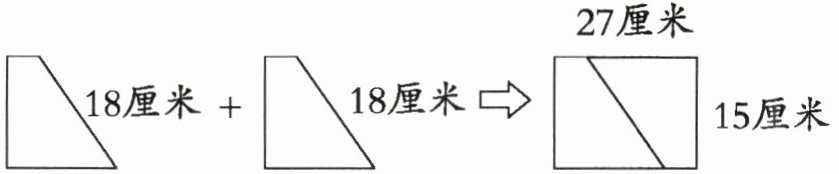
5. 如下图,两个一样的直角梯形可以拼成一个长方形,那么一个直角梯形的周长是多少厘米？

答案： 上底+下底=27厘米，直角腰=15厘米，非直角腰=18厘米。
周长=27+15+18=60厘米。
答：一个直角梯形的周长是60厘米。