《2025年小学生学习指导丛书四年级数学上册人教版》

5. 如果 1 平方米地面能站 12 个小朋友,那么 1 公顷地面大约能站(③)个小朋友。
①1200 ②12000 ③120000 ④120

答案： ③

1. (1)下列图形的面积是多少公顷?

(2)在图中画出面积为 1 公顷的正方形,并涂上颜色。

答案： 1. （1）
对于插图1：
假设插图1是一个长方形，长$a = 500$米，宽$b = 400$米。
根据长方形面积公式$S = a× b$，则$S=500×400 = 200000$（平方米）。
因为$1$公顷$ = 10000$平方米，所以$200000÷10000 = 20$（公顷）。
对于插图2：
假设插图2是一个正方形，边长$a = 300$米。
根据正方形面积公式$S=a^{2}$，则$S = 300×300=90000$（平方米）。
$90000÷10000 = 9$（公顷）。
2. （2）
因为$1$公顷$ = 10000$平方米，且正方形面积$S = a^{2}$，由$a^{2}=10000$，可得$a = 100$米。
所以画出边长为$100$米的正方形并涂色即可（具体画图略，以实际图形比例为准，画出边长为$100$米的正方形）。
综上，（1）插图1面积为$20$公顷，插图2面积为$9$公顷；（2）画出边长为$100$米的正方形（画图略）。

2. (1)下列图形的面积是多少平方千米?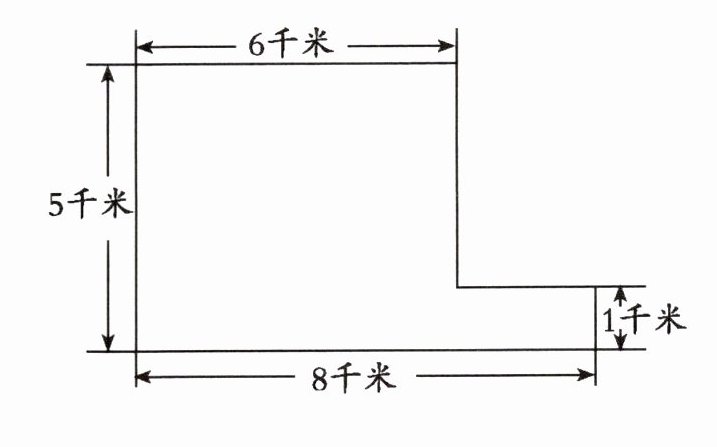
(2)在图中画出面积为 8 平方千米的长方形,并涂上颜色。

答案：
(1) 32平方千米
(2) 画一个长4千米、宽2千米的长方形（或长8千米、宽1千米等，合理即可），并涂上颜色。

1. 有一块长方形菜地,长 300 米,宽 200 米。
(1)沿着菜地的四周走一圈,要走多少千米?
(2)去年这块菜地平均每公顷种菜收入为 5000 元,这一年种菜的总收入是多少?

答案：
(1)长方形周长 = 2×(长 + 宽)= 2×(300 + 200)= 1000(米)= 1(千米)。
答：要走 1 千米。
(2)长方形面积 = 长×宽 = 300×200 = 60000(平方米)= 6(公顷)，总收入 = 6×5000 = 30000(元)。
答：这一年种菜的总收入是 30000 元。

2. 如果要将长方形菜地的长增加 200 米,宽不变(如右图所示),菜地面积增加了多少公顷?

答案： 原长方形菜地长300米，宽200米，宽不变，长增加200米后，增加的部分是一个长200米、宽200米的长方形。
根据长方形面积公式$S = a× b$（其中$S$为长方形面积，$a$为长方形的长，$b$为长方形的宽），可得增加部分的面积为：
$200×200 = 40000$（平方米）
因为1公顷 = 10000平方米，所以40000平方米 = 40000÷10000 = 4公顷。
答：菜地面积增加了4公顷。