第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
3. 将一个$40^{\circ}$的角放在 5 倍的放大镜下,在放大镜下看到的角是( )。
①$200^{\circ}$
②$8^{\circ}$
③$5^{\circ}$
④$40^{\circ}$
①$200^{\circ}$
②$8^{\circ}$
③$5^{\circ}$
④$40^{\circ}$
答案:
④
4. 李丽用破损的量角器测量角的度数(如右图),
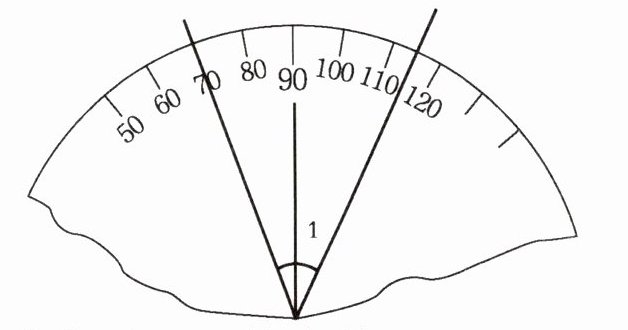
$∠1$的度数是( )。
①$35^{\circ}$
②$40^{\circ}$
③$45^{\circ}$
④$70^{\circ}$

$∠1$的度数是( )。
①$35^{\circ}$
②$40^{\circ}$
③$45^{\circ}$
④$70^{\circ}$
答案:
③
5. 杨明用量角器画了一个$135^{\circ}$的角,下列线段上能正确表示$135^{\circ}$的点是( )。

答案:
②
6. 下列说法正确的有( )。
A.角的两边张开得越大,角越大
B.一条射线长 2 米
C.过一点能画无数条直线
D.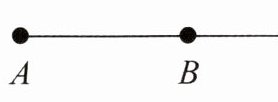
可以用射线 BA 表示
①AB
②AC
③BD
④ABD
A.角的两边张开得越大,角越大
B.一条射线长 2 米
C.过一点能画无数条直线
D.

可以用射线 BA 表示
①AB
②AC
③BD
④ABD
答案:
解:
- 选项A:角的大小与角两边张开的程度有关,角的两边张开得越大,角越大,该说法正确。
- 选项B:射线一端无限延伸,不可度量长度,所以“一条射线长$2$米”说法错误。
- 选项C:过一点能画无数条直线,该说法正确。
- 选项D:图中可以用射线$BA$表示,该说法正确。
综上,说法正确的有$ACD$。
- 选项A:角的大小与角两边张开的程度有关,角的两边张开得越大,角越大,该说法正确。
- 选项B:射线一端无限延伸,不可度量长度,所以“一条射线长$2$米”说法错误。
- 选项C:过一点能画无数条直线,该说法正确。
- 选项D:图中可以用射线$BA$表示,该说法正确。
综上,说法正确的有$ACD$。
1. 画一个$130^{\circ}$的角。
答案:
答题卡作答:
1. 先画一条射线,使量角器的中心与射线的端点重合,0°刻度线与射线重合;
2. 在量角器130°刻度线的地方点一个点;
3. 以画出的射线的端点为端点,通过刚画的点,再画一条射线;
4. 画出的两条射线所夹的角即为130°的角。
1. 先画一条射线,使量角器的中心与射线的端点重合,0°刻度线与射线重合;
2. 在量角器130°刻度线的地方点一个点;
3. 以画出的射线的端点为端点,通过刚画的点,再画一条射线;
4. 画出的两条射线所夹的角即为130°的角。
2. 画一个比直角小$20^{\circ}$的角。
答案:
1. 直角为$90^{\circ}$,所求角的度数为:$90^{\circ}-20^{\circ} = 70^{\circ}$。
2. 画角步骤:
画一条射线,使量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合。
在量角器$70^{\circ}$刻度线的地方点一个点。
以画出的射线的端点为端点,通过刚画的点,再画一条射线。
所画成的角就是$70^{\circ}$的角,即比直角小$20^{\circ}$的角。
2. 画角步骤:
画一条射线,使量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合。
在量角器$70^{\circ}$刻度线的地方点一个点。
以画出的射线的端点为端点,通过刚画的点,再画一条射线。
所画成的角就是$70^{\circ}$的角,即比直角小$20^{\circ}$的角。
3. (1)以点 A 为端点,画一条射线。(2)从点 A 开始,在这条射线上截取一条长 4 厘米的线段 AB。(3)画出一条直线 BC 与射线 AB 相交,并使相交的角为直角。
答案:
答题卡:
(1) 作图:从点A出发,用直尺画出一条射线。
(2) 作图:从点A开始,沿射线方向用直尺量取4厘米,标记为点B,得到线段AB。
(3) 作图:过点B作直线BC,使BC与AB的夹角为$90°$(使用直角三角尺或量角器确保角度为直角)。
(1) 作图:从点A出发,用直尺画出一条射线。
(2) 作图:从点A开始,沿射线方向用直尺量取4厘米,标记为点B,得到线段AB。
(3) 作图:过点B作直线BC,使BC与AB的夹角为$90°$(使用直角三角尺或量角器确保角度为直角)。
四、右图中$∠1$与$∠2$是不是相等?请说明理由。
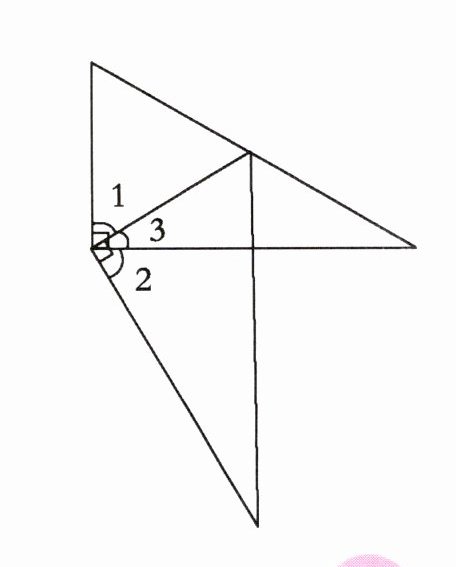

答案:
解:因为$\angle1 + \angle3 = 90^{\circ}$,所以$\angle1 = 90^{\circ}-\angle3$;
又因为$\angle2 + \angle3 = 90^{\circ}$,所以$\angle2 = 90^{\circ}-\angle3$。
根据等量代换可得$\angle1=\angle2$。
综上,$\angle1$与$\angle2$相等。
又因为$\angle2 + \angle3 = 90^{\circ}$,所以$\angle2 = 90^{\circ}-\angle3$。
根据等量代换可得$\angle1=\angle2$。
综上,$\angle1$与$\angle2$相等。
查看更多完整答案,请扫码查看


