《2025年小学生学习指导丛书四年级数学上册人教版》

1. 直接写出得数。
$70×80=$5600 $60×30=$1800 $31×20=$620 $200×12=$2400
$12×60=$720 $210×30=$6300 $30×30=$900 $320×50=$16000

答案： 5600
1800
620
2400
720
6300
900
16000

2. 用竖式计算,再用计算器验算。
$15×201=$3015 $104×30=$3120 $305×23=$6915

答案： 15×201=3015
104×30=3120
305×23=6915
验算（计算器）：
15×201=3015，正确。
104×30=3120，正确。
305×23=6915，正确。

3. 把正确答案的序号填在括号里。
(1)三位数乘两位数的积是(④)。
①三位数 ②四位数 ③五位数 ④四位数或五位数
(2)150×40的积的末尾有(②)个 0。
①2 ②3 ③1 ④无法确定
(3)与260×50的积相等的算式是(③)。
①265×60 ②280×80 ③26×500 ④52×100
(4)

(③)
①8 个百 ②80 个十 ③8 个十 ④8 个一

答案： ④②③③

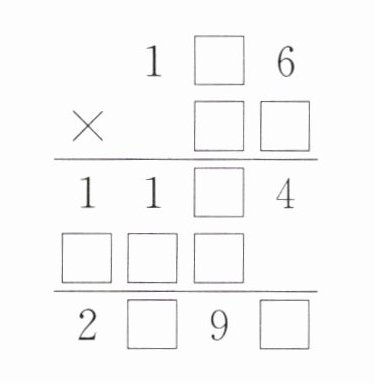
在算式的$□$内填入合适的数字,使算式成立。

219312634

答案： 1. 首先分析$1□6×□ = 11□4$：
因为$6×4 = 24$，$6×9 = 54$，假设第二个因数的个位数字是$4$，$1□6×4=11□4$，则$106×4 = 424$，$196×4=(200 - 4)×4=800 - 16 = 784$，不符合$11□4$；
假设第二个因数的个位数字是$9$，$1□6×9 = 11□4$，因为$126×9=(100 + 20+6)×9=900 + 180+54 = 1134$，所以第一个因数是$126$。
2. 然后设第二个因数的十位数字为$x$：
则$126× x$是一个三位数，且$126× x$的结果加上$1134$后得到$2□9□$。
因为$126×10 = 1260$，$126×20 = 2520$，又因为$126× x$的结果加上$1134$后千位是$2$，$126×9 = 1134$，$126×19=126×(20 - 1)=2520 - 126 = 2394$，$126×19=126×(10 + 9)=126×10+126×9=1260 + 1134$。
所以$126×19$，$□$内依次填$2$、$1$、$9$、$3$、$1$、$2$、$6$、$3$、$4$。
即$\begin{array}{r}126\\×19\\\hline1134\\126\\\hline2394\end{array}$。