《2025年假期伙伴暑假大连理工大学出版社四年级数学北师大版》

2. 解方程。
5.37+x= 13.5，解得$x$=8.13
x-5.7= 5.7，解得$x$=11.4
8x-2.4= 13.6，解得$x$=2

答案： 【解析】：
1. 对于方程$5.37 + x = 13.5$，根据等式的基本性质，等式两边同时减去一个数，等式仍然成立。为了求出$x$的值，在等式两边同时减去$5.37$，即$x = 13.5 - 5.37$，计算可得$x = 8.13$。
2. 对于方程$x - 5.7 = 5.7$，依据等式的基本性质，等式两边同时加上一个数，等式仍然成立。在等式两边同时加上$5.7$，得到$x = 5.7 + 5.7$，计算得出$x = 11.4$。
3. 对于方程$8x - 2.4 = 13.6$，首先根据等式的基本性质，等式两边同时加上$2.4$，得到$8x - 2.4 + 2.4 = 13.6 + 2.4$，化简为$8x = 16$。然后再根据等式的基本性质，等式两边同时除以$8$，即$x = 16÷8$，计算可得$x = 2$。
【答案】：$x = 8.13$；$x = 11.4$；$x = 2$

3. 用简便方法计算。
9.26+5.87+4.13
5.89×9+5.89

答案： 【解析】：
对于$9.26 + 5.87 + 4.13$，根据加法结合律$a+b+c=a+(b+c)$，先计算$5.87$与$4.13$的和，再与$9.26$相加，这样计算更简便。
对于$5.89×9 + 5.89$，可根据乘法分配律的逆运算$a× c+b× c=(a + b)× c$，把$5.89$看成$5.89×1$，则原式可转化为$5.89×(9 + 1)$进行简便计算。
【答案】：$19.26$；$58.9$

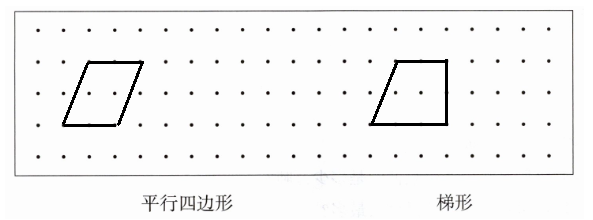
1. 在点子图上画出相应的图形。

平行四边形                                       梯形

答案：

2. 从正面、右面和上面看一看下面的立体图形,填一填。
从（上面）看
从（右面）看
从（正面）看

答案： 【解析】：通过观察立体图形，从上面看能看到两个左右排列的正方形；从右面看能看到两个上下排列的正方形；从正面看能看到三个正方形，下面两个，上面一个在左边。
【答案】：上面；右面；正面