《2025年实验班提优训练八年级数学上册苏科版》

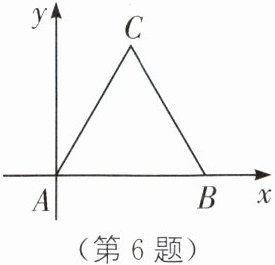
6. 如图,在等边三角形ABC中,以点A为坐标原点,AB边所在的直线为x轴建立平面直角坐标系.若点B的坐标为(2,0),求点C的坐标.
]

答案：
如图,过点C作CD⊥x轴于点D,则CD是等边三角形ABC的垂直平分线,则AD=BD,∠ADC=90°.
∵A(0,0),B(2,0),
∴AB=2,
∴AC=AB=2,
AD=1.
在Rt△ACD中,由勾股定理,得
AD²+CD²=AC².
∴CD=√(AC² - AD²)=√(2² - 1²)=√3
∴点C的坐标为(1,√3).

7. 如图,已知点A和点B的坐标分别为(1,3)和(1,-1),在线段AB上存在一点E,若OE把△AOB的面积分成1∶2的两部分,求点E的坐标.
]

答案： 设AB交x轴于点C.
∵A(1,3),B(1,−1),
∴AB=4.
∵△AOE与△BOE同高，
∴S△AOE:S△BOE=AE:BE.
∵OE把△AOB的面积分成1:2的两部分，
∴S△AOE:S△BOE=1:2或2:1.
当S△AOE:S△BOE=1:2时,AE:BE=1:2,
∴AE=1/3AB=4/3,EC=3 - 4/3=5/3,
即点E的坐标为(1,5/3);
当S△AOE:S△BOE=2:1时,AE:BE=2:1,
∴AE=2/3AB=8/3,EC=3 - 8/3=1/3,
即点E的坐标为(1,1/3).
综上所述，点E的坐标为(1,5/3)或(1,1/3).

8. 分类讨论思想 如图,A(-1,0),C(1,4),点B在x轴上,且AB= 3.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
]

答案：
(1)当点B在点A的右边时,−1 + 3 = 2;
当点B在点A的左边时,−1 - 3 = −4,
所以点B的坐标为(2,0)或(−4,0).
(2)S△ABC=1/2×3×4=6.
(3)存在.理由如下:
设点P到x轴的距离为h,
则1/2×3h = 10,解得h = 20/3.
故点P的坐标为(0,20/3)或(0,−20/3).

9. (2024·贵州中考)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为(-2,0),(0,0),则“技”所在的象限为( ).

A.第一象限
B.第二象限
C.第三象限
D.第四象限
]

答案：
A　[解析]如图，建立平面直角坐标系，则“技”在第一象限.故选A