《2025年实验班提优训练八年级数学上册苏科版》

1. 教材 P95 练习 T1·变式(2025·盐城期末)下列四组线段中,可以构成直角三角形的是(B).
A.2,3,4
B.3,4,5
C.3,4,7
D.4,5,6

答案： B

2. 已知 a,b,c 为△ABC 的三边,且满足$(a - b)·(a^2 + b^2 - c^2)= 0,$则△ABC 是(D).
A.等边三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形

答案： D　[解析]
∵(a - b)(a² + b² - c²) = 0,
∴a - b = 0或a² + b² - c² = 0,即a = b或a² + b² = c².
∴△ABC为等腰三角形或直角三角形.故选D.

3. 传统文化 《九章算术》(2023·泸州中考)《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数 a,b,c 的计算公式:$a= \frac{1}{2}(m^2 - n^2)$,$b= mn$,$c= \frac{1}{2}(m^2 + n^2)$,其中 $m ＞ n ＞ 0$,m,n 是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是(C).
A.3,4,5
B.5,12,13
C.6,8,10
D.7,24,25

答案： C　[解析]
∵当m = 3,n = 1时,
　a = $\frac{1}{2}$(m² - n²) = $\frac{1}{2}$×(3² - 1²) = 4,b = mn = 3×1 = 3,c = $\frac{1}{2}$(m² + n²) = $\frac{1}{2}$×(3² + 1²) = 5,
∴选项A不符合题意;
∵当m = 5,n = 1时,a = $\frac{1}{2}$(m² - n²) = $\frac{1}{2}$×(5² - 1²) = 12,b = mn = 5×1 = 5,c = $\frac{1}{2}$(m² + n²) = $\frac{1}{2}$×(5² + 1²) = 13,
∴选项B不符合题意;
∵当m = 7,n = 1时,a = $\frac{1}{2}$(m² - n²) = $\frac{1}{2}$×(7² - 1²) = 24,b = mn = 7×1 = 7,c = $\frac{1}{2}$(m² + n²) = $\frac{1}{2}$×(7² + 1²) = 25,
∴选项D不符合题意;
∵没有符合条件的m,n使a,b,c各为6,8,10,
∴选项C符合题意.故选C;

4.(2025·宿迁宿豫区期中改编)如图是搭建帐篷的示意图.在△ABC 中,支架 AD 从帐篷顶点 A 支撑在水平的支架 BC 上,且 AD⊥BC 于点 D,经测量得:AB = 2 m,AD = 1.2 m,CD = 0.9 m.按照要求,帐篷支架 AB 与 AC 所夹的角需为直角,请通过计算说明学生搭建的帐篷是否符合条件.

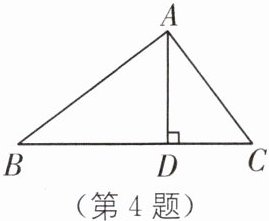
答案： 帐篷符合要求.理由如下:
　在Rt△ACD中,CD = 0.9m,AD = 1.2m,
∴AC = $\sqrt{AD² + CD²}$ = $\sqrt{1.2² + 0.9²}$ = 1.5(m),
　在Rt△ADB中,AB = 2m,AD = 1.2m,
∴BD = $\sqrt{2² - 1.2²}$ = 1.6(m),
∴BC = 1.6 + 0.9 = 2.5(m).
∵AB² + AC² = 2² + 1.5² = 6.25,BC² = 2.5² = 6.25,
∴AB² + AC² = BC².
∴△ABC是直角三角形,∠BAC = 90°.
∴帐篷符合要求.

5. 教材 P96 习题 T1·变式(2024·苏州吴中区期中)下列由三条线段 a,b,c(所对的角分别为∠A,∠B,∠C)构成的三角形:①∠A + ∠B = ∠C；②$a = 3k$,$b = 4k$,$c = 5k$($k ＞ 0$)；③∠A : ∠B : ∠C = 3 : 4 : 5；④$a = m^2 + 1$,$b = m^2 - 1$,$c = 2m$(m 为大于 1 的整数),其中能构成直角三角形的是(B).
A.①④
B.①②④
C.②③④
D.①②③

答案： B　[解析]①
∵∠A + ∠B = ∠C,∠A + ∠B + ∠C = 180°,
∴∠C + ∠C = 180°,
∴∠C = 90°,
∴能构成直角三角形;
　②
∵a² + b² = (3k)² + (4k)² = 25k²,c² = (5k)² = 25k²,
∴a² + b² = c²,
∴能构成直角三角形;
　③
∵∠A:∠B:∠C = 3:4:5,∠A + ∠B + ∠C = 180°,
∴∠C = 180°×$\frac{5}{12}$ = 75°,
∴不能构成直角三角形;
　④
∵a² = (m² + 1)² = m⁴ + 2m² + 1,b² + c² = (m² - 1)² + (2m)² = m⁴ - 2m² + 1 + 4m² = m⁴ + 2m² + 1,
∴a² = b² + c²,
∴能构成直角三角形.
∴能构成直角三角形的是①②④.故选B
　归纳总结　本题考查了勾股定理的逆定理、三角形内角和定理，熟练掌握勾股定理的逆定理以及三角形内角和定理是解题的关键.

6. 实验班原创 已知三条线段分别长 s,t,h,且满足$(s + t)(s - t)= h^2$,则以这三条线段为边组成的三角形为直角三角形.

答案： 直角三角形

7.(2025·宿迁期末)如图,在“4×4”的正方形网格中,∠1 + ∠2 的度数为______.

答案：
45°　[解析]将∠2向下平移1个单位格得到AB,如图,连接AC,
∴∠2 = ∠ABE.
∵AC² = AD² + CD² = 2² + 1² = 5,
　AB² = BE² + AE² = 2² + 1² = 5,BC² = 3² + 1² = 10,
∴AC² + AB² = BC²,
∴△ABC是等腰直角三角形,
∴∠ABC = 45°,
∴∠ABE + ∠1 = 45°,
∴∠1 + ∠2 = 45°.
　

8. 若 a,b,c 是直角三角形的三条边长,斜边 c 上的高是 h,给出下列结论:①以$a^2$,$b^2$,$c^2$的长为边的三条线段能组成一个三角形；②以$a + b$,$c + h$,h 的长为边的三条线段能组成直角三角形；③以$\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$的长为边的三条线段能组成直角三角形.其中所有正确结论的序号为______②.

答案： ②

9. 中考新考法 新定义问题 定义:如图,点 M,N 把线段 AB 分割成 AM,MN,NB,若以 AM,MN,NB 为边的三角形是一个直角三角形,则称点 M,N 是线段 AB 的勾股分割点.

(1)已知 M,N 把线段 AB 分割成 AM,MN,NB,若 AM = 1.5,MN = 2.5,BN = 2,则点 M,N 是线段 AB 的勾股分割点吗？请说明理由.
(2)已知点 M,N 是线段 AB 的勾股分割点,且 AM 为直角边,若 AB = 24,AM = 6,求 BN 的长.

答案：
(1)是.理由如下:
∵AM² + BN² = 1.5² + 2² = 6.25,MN² = 2.5² = 6.25,
∴AM² + NB² = MN²,
∴以AM,MN，NB为边的三角形是一个直角三角形，
∴点M,N是线段AB的勾股分割点.
(2)设BN = x,则MN = 24 - AM - BN = 18 - x.
　①当MN为最长线段时,
　由题意,得MN² = AM² + NB²,
　即(18 - x)² = x² + 36,解得x = 8;
　②当BN为最长线段时,
　由题意,得BN² = AM² + MN²,
　即x² = 36 + (18 - x)²,解得x = 10.
　综上所述，BN的长为8或10.
　易错警示　本题考查了勾股定理的逆定理的运用，解题的关键是理解题意，学会分类讨论，注意不能漏解，属于中考常考题型.