《2025年实验班提优训练八年级数学上册苏科版》

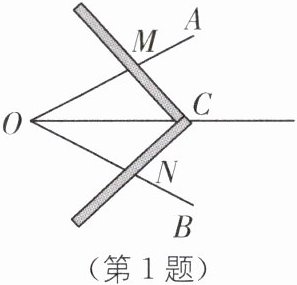
1. 工人师傅常用角尺平分一个任意角,做法如下：如图,∠AOB是一个任意角,在边OA,OB上分别取OM= ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线. 工人师傅这么做的原理是一种三角形全等的判定方法,这种判定方法是(A).

A.SSS
B.SAS
C.ASA
D.AAS

答案： 【解析】：
首先，由题意知，工人师傅在边$OA$和$OB$上分别取了$OM = ON$，这是第一组等长的边。
接着，移动角尺，使角尺两边相同的刻度分别与点$M$和$N$重合，这意味着角尺到点$M$和$N$的距离是相等的，即$CM = CN$，这是第二组等长的边。
最后，由于角尺的两边分别与$M$和$N$重合，并且顶点为$C$，所以$OC$是两个三角形$\triangle OMC$和$\triangle ONC$的公共边，即$OC = OC$，这是第三组等长的边。
根据三角形全等的判定方法，当三个边分别相等时，两个三角形全等，即$\triangle OMC \cong \triangle ONC(SSS)$。
由于两个三角形全等，所以它们对应的角也相等，即$\angle MOC = \angle NOC$，从而证明了$OC$是$\angle AOB$的平分线。
【答案】：A

2. 传统文化 油纸伞(2025·南京联合体期中)我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识. 如图是油纸伞的张开示意图,AE= AF,GE= GF,则△AEG≌△AFG的依据是(D).
A.SAS
B.ASA
C.AAS
D.SSS

答案： 证明：在△AEG和△AFG中，
∵AE=AF，GE=GF，AG=AG，
∴△AEG≌△AFG（SSS）。
D

3. 教材P26练习T1·变式 如图,在△ABC和△ABD中,AC与BD相交于点E,AD= BC,AC= BD. 求证：∠C= ∠D.

答案： 【解析】：本题考查全等三角形的判定定理。在两个三角形中，如果已知三边对应相等，那么根据“边边边”（SSS）判定定理，这两个三角形是全等的。全等三角形的对应角相等，因此可以证明∠C= ∠D。
【答案】：证明：
连接AB。
在△ABC和△BAD中，
$ \begin{aligned}AB &= BA \quad (公共边) ,\\BC &= AD \quad (已知) ,\\AC &= BD \quad (已知)\end{aligned} $
$ \therefore \triangle ABC \cong \triangle BAD \quad (SSS) $。
$ \therefore \angle C = \angle D $。

4.(2025·福建厦门期中)安装空调一般会采用如图的方法固定,其依据的几何原理是(三角形具有稳定性).

答案： 【解析】：
本题考察的是全等三角形的判定在实际生活中的应用。在安装空调时，通常会采用三角形结构来固定，这是因为三角形具有稳定性，即三角形的三个边和三个角相互制约，使得三角形在受到外力作用时不易变形。这种稳定性是由全等三角形的性质决定的，即全等三角形的对应边和对应角都相等，从而保证了三角形的稳定性。
【答案】：
三角形具有稳定性。

5.(2024·徐州期末)如图,已知$AB = AD$,要使$\triangle ABC\cong\triangle ADC$(SSS),只需补充一个条件______BC=DC.

答案： BC=DC [解析]在△ABC和△ADC中，{AB=AD，BC=DC，AC=AC，
∴△ABC≌△ADC(SSS).

6.(教材P32习题T8·变式)(2024·常州新北区期中)如图,$AB = DC$,$AC = DB$,$AC$,$DB交于点O$,$\angle AOB与\angle OBC$有怎样的数量关系？证明你的结论.

答案： ∠AOB=2∠OBC. 理由如下：在△ABC和△DCB中，{AB=DC，AC=DB，BC=CB，
∴△ABC≌△DCB(SSS).
∴∠ACB=∠DBC.
∵∠AOB=∠OBC+∠OCB，
∴∠AOB=2∠OBC.

7. 如图,已知$AB = AD$,$BC = DC$,$E$,$F分别是DC$,$BC$的中点,求证：$AE = AF$.

答案： 连接AC.在△ACD和△ACB中，{AD=AB，AC=AC，CD=CB，
∴△ACD≌△ACB(SSS)，
∴∠ACE=∠ACF.
∵BC=DC，E，F分别是DC，BC的中点，
∴CE=CF.在△ACE和△ACF中，{CE=CF，∠ACE=∠ACF，AC=AC，
∴△ACE≌△ACF(SAS)，
∴AE=AF.