第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. (2024·德阳中考)正比例函数 $y= kx(k≠0)$ 的图象如图所示,则 $k$ 的值可能是(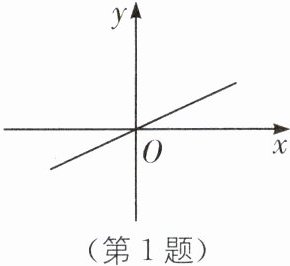
A.$\frac{1}{2}$
B.$-\frac{1}{2}$
C.$-1$
D.$-\frac{1}{3}$
A
).
A.$\frac{1}{2}$
B.$-\frac{1}{2}$
C.$-1$
D.$-\frac{1}{3}$
答案:
A [解析]由图象知,函数值y随x的增大而增大,
∴k>0,
∴k的值可能是$\frac{1}{2}$.故选A.
∴k>0,
∴k的值可能是$\frac{1}{2}$.故选A.
2. 下列各点中,在正比例函数 $y= 2x$ 的图象上的是(
A.$(-5,4)$
B.$(-3.5,1)$
C.$(4,8)$
D.$(1008,2025)$
C
).A.$(-5,4)$
B.$(-3.5,1)$
C.$(4,8)$
D.$(1008,2025)$
答案:
C
3. 正比例函数 $y= \frac{1}{2}x$ 的图象是经过点 $(0,$
0
$)$ 和点 $(1,$$\frac{1}{2}$
$)$ 的一条直线,一次函数 $y= 2x-1$ 的图象是经过点 $(0,$-1
$)$ 的一条直线.
答案:
0 $\frac{1}{2}$ -1
4. 教材 P153 练习·变式 已知函数 $y= -\frac{2}{3}x$ 的图象,利用图象,求当 $x= 4.5$ 时,$y$ 的值以及当 $y= -6$ 时,$x$ 的值.
答案:
∵$y=-\frac{2}{3}x$,
∴当$x=0$时,$y=0$;当$x=3$时,$y=-2$.
∴函数$y=-\frac{2}{3}x$的图象经过点$(0,0)$和$(3,-2)$.当$x=4.5$时,$y=-3$;当$y=-6$时,$x=9$.
∵$y=-\frac{2}{3}x$,
∴当$x=0$时,$y=0$;当$x=3$时,$y=-2$.
∴函数$y=-\frac{2}{3}x$的图象经过点$(0,0)$和$(3,-2)$.当$x=4.5$时,$y=-3$;当$y=-6$时,$x=9$.
5. 跨学科 液体压强 (2024·广安中考)向如图所示的空容器内匀速注水,从水刚接触底部时开始计时,直至把容器注满,在注水过程中,设容器内底部所受水的压强为 $y$(单位:帕),时间为 $x$(单位:秒),则 $y$ 关于 $x$ 的函数图象大致为(
B
).
答案:
B [解析]因为根据图象可知,底层圆柱的直径较大,上层圆柱的直径较小,所以注水过程中容器内底部所受水的压强变化是先慢后快.故选项B正确.故选B.
6. 小妍从家出发步行上学,途中发现忘带了数学书,于是打电话让妈妈马上从家里沿上学的路送来,同时小妍也掉头往家走,遇到妈妈后聊了一会儿,接着继续向学校走去. 设小妍从家出发后所用时间为 $t$,小妍与学校的距离为 $s$,下面能反映 $s$ 与 $t$ 的函数关系的大致图象是(
B
).
答案:
B [解析]小妍从出发到发现忘了带数学书的这段时间,s逐渐减小;小妍往回走遇到妈妈的这段时间内,s逐渐增加;两人聊天的这段时间,s保持不变;小妍继续走前往学校的这段时间,s逐渐减小到0,所以能反映s与t的函数关系的大致图象是B.故选B.思路引导:本题主要考查了函数的图象,要熟练掌握,解答此题的关键是弄清楚小妍与学校的距离s随着时间t的增加的变化情况.
查看更多完整答案,请扫码查看


