第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是(
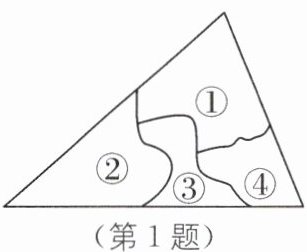
A.带①②去
B.带②③去
C.带③④去
D.带②④去
A
). 
A.带①②去
B.带②③去
C.带③④去
D.带②④去
答案:
A [解析]A. 带①②去,符合 ASA 判定,选项符合题意;B. 带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;C. 带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;D. 带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意.故选 A.
2.(2024·宿迁宿豫区期中)如图,虽然三角形被纸板挡住了一部分,但是小明仍能画出一个能与这个三角形完全重合的三角形,其数学依据是(

A.ASA
B.SAS
C.SSS
D.SSA
A
). 
A.ASA
B.SAS
C.SSS
D.SSA
答案:
A
3.(中考新考法 满足结论的条件开放)如图,点 B,F,C,E 在一条直线上,AB//ED,AC//FD,要使△ABC≌△DEF,只需添加一个条件,则这个条件可以是

BC=EF(答案不唯一)
.
答案:
BC=EF(答案不唯一) [解析]
∵AB//ED,
∴∠B=∠E.
∵AC//DF,
∴∠ACB=∠DFE.在△ABC 和△DEF 中,{∠ACB=∠DFE,BC=EF,∠B=∠E,}
∴△ABC≌△DEF(ASA).
∵AB//ED,
∴∠B=∠E.
∵AC//DF,
∴∠ACB=∠DFE.在△ABC 和△DEF 中,{∠ACB=∠DFE,BC=EF,∠B=∠E,}
∴△ABC≌△DEF(ASA).
4.(教材 P20 练习 T2·变式)(2025·宿迁宿豫区期中)如图,AN 与 MB 相交于点 O,OA= OM,∠A= ∠M. 求证:AB= MN.


答案:
∵AN 与 MB 相交于点 O,
∴∠AOB=∠MON.在△AOB 和△MON 中,{∠A=∠M,OA=OM,∠AOB=∠MON,}
∴△AOB≌△MON(ASA),
∴AB=MN.
∵AN 与 MB 相交于点 O,
∴∠AOB=∠MON.在△AOB 和△MON 中,{∠A=∠M,OA=OM,∠AOB=∠MON,}
∴△AOB≌△MON(ASA),
∴AB=MN.
5.(2024·扬州江都三中月考)如图,点 A,C,B,D 在同一条直线上,BE//DF,∠A= ∠F,AB= FD. 若∠FCD= 30°,∠A= 80°,则∠DBE 的度数为

110
°.
答案:
110 [解析]
∵BE//DF,
∴∠ABE=∠D.在△ABE 和△FDC 中,{∠A=∠F,AB=FD,∠ABE=∠D,}
∴△ABE≌△FDC(ASA),
∴∠E=∠FCD=30°,
∴∠DBE=∠E+∠A=30°+80°=110°.
∵BE//DF,
∴∠ABE=∠D.在△ABE 和△FDC 中,{∠A=∠F,AB=FD,∠ABE=∠D,}
∴△ABE≌△FDC(ASA),
∴∠E=∠FCD=30°,
∴∠DBE=∠E+∠A=30°+80°=110°.
6. 如图,∠1= ∠2,∠3= ∠4,欲说明 BC= BD,须先知
△ACE
≌△ADE
,再说明△ACB
≌△ADB
;欲说明 CE= DE,须先知△ACE
≌△ADE
.
答案:
△ACE △ADE △ACB(或△CEB) △ADB(或△DEB) △ACE △ADE.
7.(新情境 利用三角形全等测河宽)(2025·河北唐山路北区期中)如图,要测量河两岸相对的 A,B 两点之间的距离,可以在与 AB 垂直的河岸 BF 上取 C,D 两点,且使 BC= CD. 从点 D 出发沿与河岸 BF 垂直的方向移动到点 E,使点 A,C,E 在一条直线上. 若测量 DE 的长为 25 米,则 A,B 两点之间的距离为
25
米.
答案:
25 [解析]
∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90°.在△ABC 和△EDC 中,{∠ABC=∠EDC,BC=DC,∠ACB=∠ECD,}
∴△ABC≌△EDC(ASA),
∴AB=DE=25 米,即 A,B 两点之间的距离为 25 米.
∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90°.在△ABC 和△EDC 中,{∠ABC=∠EDC,BC=DC,∠ACB=∠ECD,}
∴△ABC≌△EDC(ASA),
∴AB=DE=25 米,即 A,B 两点之间的距离为 25 米.
8.(8 字型)(2024·苏州高新区一模)如图,∠A= ∠B,AE= BE,点 D 在 AC 边上,∠1= ∠2,AE 和 BD 相交于点 O.
(1)求证:△AEC≌△BED;
(2)若∠1= 38°,求∠BDE 的度数.

(1)求证:△AEC≌△BED;
(2)若∠1= 38°,求∠BDE 的度数.

答案:
(1)
∵AE 和 BD 相交于点 O,
∴∠AOD=∠BOE.又∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.在△AEC 和△BED 中,{∠A=∠B,AE=BE,∠AEC=∠BED,}
∴△AEC≌△BED(ASA).
(2)
∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.在△EDC 中,
∵EC=ED,∠1=38°,
∴∠C=∠EDC=71°,
∴∠BDE=∠C=71°.归纳总结 本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
(1)
∵AE 和 BD 相交于点 O,
∴∠AOD=∠BOE.又∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.在△AEC 和△BED 中,{∠A=∠B,AE=BE,∠AEC=∠BED,}
∴△AEC≌△BED(ASA).
(2)
∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.在△EDC 中,
∵EC=ED,∠1=38°,
∴∠C=∠EDC=71°,
∴∠BDE=∠C=71°.归纳总结 本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
查看更多完整答案,请扫码查看


