第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
【例1】(第七届“学用杯”全国数学知识应用竞赛初赛)如图所示的徽标,是我国古代弦图的变形,该图是由其中的一个Rt△ABC绕中心点O顺时针连续旋转3次,每次旋转90°得到的,如果中间小正方形的面积为1cm^2,这个图形的总面积为113cm^2,且AD= 2cm,请问徽标的外围周长为______
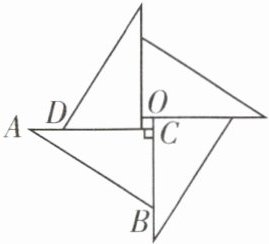
解析:设Rt△ABC的较长直角边为a,较短直角边为b,斜边为c。
依题意,得a - b= 3,$\frac{1}{2}ab= \frac{113 - 1}{4}$。
又由勾股定理,得$c^2= a^2 + b^2= (a - b)^2 + 2ab= 3^2 + 112= 121$,
所以c= 11cm。
所以徽标的外围周长= 4×(11 + 2)= 52(cm)。
答案:52
52
cm。
解析:设Rt△ABC的较长直角边为a,较短直角边为b,斜边为c。
依题意,得a - b= 3,$\frac{1}{2}ab= \frac{113 - 1}{4}$。
又由勾股定理,得$c^2= a^2 + b^2= (a - b)^2 + 2ab= 3^2 + 112= 121$,
所以c= 11cm。
所以徽标的外围周长= 4×(11 + 2)= 52(cm)。
答案:52
答案:
【解析】:本题可先根据中间小正方形的面积得出边长,进而得到$a - b$的值,再结合图形总面积求出$\frac{1}{2}ab$的值,最后利用勾股定理求出斜边$c$的值,从而计算出徽标的外围周长。
1. 求$a - b$的值:
已知中间小正方形的面积为$1cm^2$,根据正方形面积公式$S = 边长×边长$,可得中间小正方形的边长为$1cm$,由图可知$AD$的长度等于较长直角边$a$减去较短直角边$b$,即$a - b = AD = 2 + 1 = 3cm$。
2. 求$\frac{1}{2}ab$的值:
已知该图形的总面积为$113cm^2$,中间小正方形面积为$1cm^2$,那么四个直角三角形的面积之和为$113 - 1 = 112cm^2$,所以一个直角三角形的面积为$\frac{113 - 1}{4}cm^2$,又因为直角三角形面积公式为$S = \frac{1}{2}ab$,所以$\frac{1}{2}ab = \frac{113 - 1}{4}$。
3. 求斜边$c$的值:
根据勾股定理$c^2 = a^2 + b^2$,而$a^2 + b^2$可变形为$(a - b)^2 + 2ab$,将$a - b = 3$,$\frac{1}{2}ab = \frac{113 - 1}{4}$代入可得:
$c^2 = (a - b)^2 + 2ab = 3^2 + 112 = 121$,
因为$c$为三角形的边长,即$c\gt0$,所以对$c^2 = 121$两边同时开平方可得$c = 11cm$。
4. 计算徽标的外围周长:
观察图形可知,徽标的外围由$4$条长度为$c$的线段和$4$条长度为$AD$的线段组成,已知$c = 11cm$,$AD = 2cm$,所以徽标的外围周长为$4×(11 + 2) = 52cm$。
【答案】:52
1. 求$a - b$的值:
已知中间小正方形的面积为$1cm^2$,根据正方形面积公式$S = 边长×边长$,可得中间小正方形的边长为$1cm$,由图可知$AD$的长度等于较长直角边$a$减去较短直角边$b$,即$a - b = AD = 2 + 1 = 3cm$。
2. 求$\frac{1}{2}ab$的值:
已知该图形的总面积为$113cm^2$,中间小正方形面积为$1cm^2$,那么四个直角三角形的面积之和为$113 - 1 = 112cm^2$,所以一个直角三角形的面积为$\frac{113 - 1}{4}cm^2$,又因为直角三角形面积公式为$S = \frac{1}{2}ab$,所以$\frac{1}{2}ab = \frac{113 - 1}{4}$。
3. 求斜边$c$的值:
根据勾股定理$c^2 = a^2 + b^2$,而$a^2 + b^2$可变形为$(a - b)^2 + 2ab$,将$a - b = 3$,$\frac{1}{2}ab = \frac{113 - 1}{4}$代入可得:
$c^2 = (a - b)^2 + 2ab = 3^2 + 112 = 121$,
因为$c$为三角形的边长,即$c\gt0$,所以对$c^2 = 121$两边同时开平方可得$c = 11cm$。
4. 计算徽标的外围周长:
观察图形可知,徽标的外围由$4$条长度为$c$的线段和$4$条长度为$AD$的线段组成,已知$c = 11cm$,$AD = 2cm$,所以徽标的外围周长为$4×(11 + 2) = 52cm$。
【答案】:52
【例2】(第二十一届省初中数学竞赛)一个直角三角形三边的长a,b,c都是整数,且满足a < b < c,a + c= 49,则这个直角三角形的面积为______
210
。
答案:
解:
∵直角三角形三边的长a,b,c都是整数,且满足a < b < c,a + c= 49,
∴由勾股定理得$a^2 + b^2 = c^2$,
$a^2 + b^2 = (49 - a)^2$,
展开得$a^2 + b^2 = 2401 - 98a + a^2$,
化简得$b^2 = 2401 - 98a = 49×(49 - 2a)$。
∵b为整数,
∴49 - 2a必为完全平方数,设$49 - 2a = k^2$(k为正整数),
则$k^2$的值可能为1,4,9,16,25,36,
当$k^2 = 1$时,49 - 2a = 1,解得a=24,c=49 - 24=25,此时b²=49×1=49,b=7,
∵24<7不成立,舍去;
当$k^2 = 4$时,49 - 2a = 4,解得a=22.5,不是整数,舍去;
当$k^2 = 9$时,49 - 2a = 9,解得a=20,c=49 - 20=29,b²=49×9=441,b=21,
∵20<21<29,成立;
当$k^2 = 16$时,49 - 2a = 16,解得a=16.5,不是整数,舍去;
当$k^2 = 25$时,49 - 2a = 25,解得a=12,c=49 - 12=37,b²=49×25=1225,b=35,
∵12<35<37,成立;
当$k^2 = 36$时,49 - 2a = 36,解得a=6.5,不是整数,舍去。
综上,a=20,b=21,c=29或a=12,b=35,c=37,
面积为$\frac{1}{2}×20×21=210$或$\frac{1}{2}×12×35=210$。
答:这个直角三角形的面积为210。
∵直角三角形三边的长a,b,c都是整数,且满足a < b < c,a + c= 49,
∴由勾股定理得$a^2 + b^2 = c^2$,
$a^2 + b^2 = (49 - a)^2$,
展开得$a^2 + b^2 = 2401 - 98a + a^2$,
化简得$b^2 = 2401 - 98a = 49×(49 - 2a)$。
∵b为整数,
∴49 - 2a必为完全平方数,设$49 - 2a = k^2$(k为正整数),
则$k^2$的值可能为1,4,9,16,25,36,
当$k^2 = 1$时,49 - 2a = 1,解得a=24,c=49 - 24=25,此时b²=49×1=49,b=7,
∵24<7不成立,舍去;
当$k^2 = 4$时,49 - 2a = 4,解得a=22.5,不是整数,舍去;
当$k^2 = 9$时,49 - 2a = 9,解得a=20,c=49 - 20=29,b²=49×9=441,b=21,
∵20<21<29,成立;
当$k^2 = 16$时,49 - 2a = 16,解得a=16.5,不是整数,舍去;
当$k^2 = 25$时,49 - 2a = 25,解得a=12,c=49 - 12=37,b²=49×25=1225,b=35,
∵12<35<37,成立;
当$k^2 = 36$时,49 - 2a = 36,解得a=6.5,不是整数,舍去。
综上,a=20,b=21,c=29或a=12,b=35,c=37,
面积为$\frac{1}{2}×20×21=210$或$\frac{1}{2}×12×35=210$。
答:这个直角三角形的面积为210。
1.(“学用杯”全国数学知识应用竞赛初赛)为了美化环境,净化城市的天空,某市要将建在西里(城中村)的一座高50m的烟囱拆除,由于烟囱附近的房子密集,拆除只能采取分段拆除,若烟囱折断时,顶端下来正好砸在距烟囱底部10m的地方最安全,那么按以上要求该烟囱应从底部向上
24
m处折断。
答案:
1. 24 [解析]设应从底部向上x米处折断,则另外两边分别为(50-x)米,10米,由勾股定理,得$10^{2}+x^{2}=(50-x)^{2}$,解得x=24.故烟囱应从底部向上24米处折断.
2.(时代学习报数学文化复赛)如图(1)是一面长方形彩旗完全展平时的示意图(单位:cm),其中长方形ABCD是由白布缝制的穿旗杆用的旗裤,阴影部分CDEF为长方形绸缎旗面,如图(2),将穿好彩旗的旗杆垂直插在操场上,旗杆顶端到地面的高度为220cm,在无风的天气里,求彩旗自然下垂时最低处离地面的高度h。


答案:
2. 如图,连接DF.
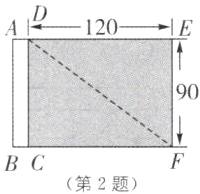
在Rt△DEF中,
∵EF=90cm,ED=120cm,
∴$DF^{2}=EF^{2}+DE^{2}=90^{2}+120^{2}=22500$,
∴DF=150cm,
∴h=220-150=70(cm).故在无风的天气里,彩旗自然下垂时最低处离地面的高度h为70cm.
2. 如图,连接DF.

在Rt△DEF中,
∵EF=90cm,ED=120cm,
∴$DF^{2}=EF^{2}+DE^{2}=90^{2}+120^{2}=22500$,
∴DF=150cm,
∴h=220-150=70(cm).故在无风的天气里,彩旗自然下垂时最低处离地面的高度h为70cm.
查看更多完整答案,请扫码查看


