第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. 给出下列四个说法:①任何图形都有对称轴;②等腰三角形属于轴对称图形;③若△ABC与△A′B′C′关于直线m对称,则△ABC与△A′B′C′全等;④角的对称轴是角的平分线. 其中正确的个数是(
A.1
B.2
C.3
D.4
B
).A.1
B.2
C.3
D.4
答案:
B
2.(2024·南通期中)如图,在Rt△ABC中,∠BAC= 90°,∠ABC的平分线交AC于点D,DE⊥BC于点E,若△ABC与△CDE的周长分别为13和3,则AB的长为(
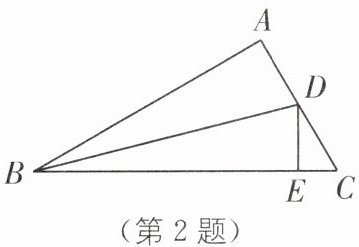
A.10
B.16
C.8
D.5
]
D
).
A.10
B.16
C.8
D.5
]
答案:
D [解析]
∵∠BAC=90°,BD平分∠ABC,DE⊥BC,
∴AD=DE. 在Rt△ABD和Rt△EBD中,{BD=BD,AD=ED},
∴Rt△ABD≌Rt△EBD(HL),
∴AB=BE.
∵△ABC与△CDE的周长分别为13和3,
∴AB+BC+AC=AB+AC+BE+EC=13,DE+EC+DC=AD+EC+DC=AC+EC=3,
∴AB+BE=10,
∴AB=BE=5. 故选D.
∵∠BAC=90°,BD平分∠ABC,DE⊥BC,
∴AD=DE. 在Rt△ABD和Rt△EBD中,{BD=BD,AD=ED},
∴Rt△ABD≌Rt△EBD(HL),
∴AB=BE.
∵△ABC与△CDE的周长分别为13和3,
∴AB+BC+AC=AB+AC+BE+EC=13,DE+EC+DC=AD+EC+DC=AC+EC=3,
∴AB+BE=10,
∴AB=BE=5. 故选D.
3. 如图,在Rt△ABC中,∠C= 90°,AD平分∠BAC交BC于点D,AB= 10,S△ABD= 15,则CD的长为( ).

A.3
B.4
C.5
D.6
]

A.3
B.4
C.5
D.6
]
答案:
A [解析]如图,过点D作DE⊥AB于点E.
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=$\frac{1}{2}$AB·DE=$\frac{1}{2}$×10DE=15, 解得DE=3,
∴CD=3.故选A.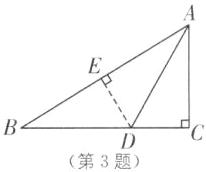
A [解析]如图,过点D作DE⊥AB于点E.
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=$\frac{1}{2}$AB·DE=$\frac{1}{2}$×10DE=15, 解得DE=3,
∴CD=3.故选A.

4.(2025·常州武进区期中)如图,AC平分∠BAD,CD⊥AD于点D,CE⊥AB于点E,点F在AD上,点E在AB上,且CF= CB.
(1)求证:BE= DF;
(2)若CE= 6,AD= 8,求四边形ABCF的面积.
]

(1)求证:BE= DF;
(2)若CE= 6,AD= 8,求四边形ABCF的面积.
]

答案:
(1)
∵AC平分∠BAD,CE⊥AB,CD⊥AD,
∴CD=CE.
∵∠D=∠CEB=∠CEA=90°. 在Rt△CDF和Rt△CEB中,{CF=CB,CD=CE},
∴Rt△CDF≌Rt△CEB(HL),
∴BE=DF.
(2)
∵Rt△CDF≌Rt△CEB,
∴S△CDF=S△CEB,
∴四边形ABCF的面积=四边形AECD的面积,在Rt△AEC和Rt△ADC中,{AC=AC,CD=CE},
∴Rt△AEC≌Rt△ADC(HL),
∴S△AEC=S△ADC.
∵S△ADC=$\frac{1}{2}$AD·CD=24,
∴S四边形ABCF=2S△ADC=48. 归纳总结 本题考查了全等三角形的判定和性质、角平分线的性质,熟练掌握全等三角形的判定和性质定理是解题的关键
(1)
∵AC平分∠BAD,CE⊥AB,CD⊥AD,
∴CD=CE.
∵∠D=∠CEB=∠CEA=90°. 在Rt△CDF和Rt△CEB中,{CF=CB,CD=CE},
∴Rt△CDF≌Rt△CEB(HL),
∴BE=DF.
(2)
∵Rt△CDF≌Rt△CEB,
∴S△CDF=S△CEB,
∴四边形ABCF的面积=四边形AECD的面积,在Rt△AEC和Rt△ADC中,{AC=AC,CD=CE},
∴Rt△AEC≌Rt△ADC(HL),
∴S△AEC=S△ADC.
∵S△ADC=$\frac{1}{2}$AD·CD=24,
∴S四边形ABCF=2S△ADC=48. 归纳总结 本题考查了全等三角形的判定和性质、角平分线的性质,熟练掌握全等三角形的判定和性质定理是解题的关键
5. 如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于点E,PF⊥OD于点F. 下列结论:①PE= PF;②点P在∠COD的平分线上;③∠APB= 90°-∠O. 其中正确的有( ).

A.0个
B.1个
C.2个
D.3个
]

A.0个
B.1个
C.2个
D.3个
]
答案:
C [解析]①如图,过点P作PH⊥AB于点H.
∵AP是∠CAB的平分线,且PH⊥AB,PE⊥AC,
∴PE=PH.
∵BP平分∠ABD,且PH⊥BA,PF⊥BD,
∴PF=PH,
∴PE=PF,
∴①正确; ②由①可知PE=PF, 又PE⊥OC于点E,PF⊥OD于点F,
∴点P在∠COD的平分线上,
∴②正确; ③
∵∠O+∠OEP+∠EPF+∠OFP=360°, 又∠OEP+∠OFP=90°+90°=180°,
∴∠O+∠EPF=180°,即∠O+∠EPA+∠HPA+∠HPB+∠FPB=180°.
∵PE=PH,PA=PA,PE⊥AC,PH⊥AB,
∴△PEA≌△PHA(HL),
∴∠EPA=∠HPA. 同理,∠FPB=∠HPB,
∴∠O+2(∠HPA+∠HPB)=180°, 即∠O+2∠APB=180°,
∴∠APB=90°−$\frac{1}{2}$∠O.
∴③错误.故选C;
C [解析]①如图,过点P作PH⊥AB于点H.
∵AP是∠CAB的平分线,且PH⊥AB,PE⊥AC,
∴PE=PH.
∵BP平分∠ABD,且PH⊥BA,PF⊥BD,
∴PF=PH,
∴PE=PF,
∴①正确; ②由①可知PE=PF, 又PE⊥OC于点E,PF⊥OD于点F,
∴点P在∠COD的平分线上,
∴②正确; ③
∵∠O+∠OEP+∠EPF+∠OFP=360°, 又∠OEP+∠OFP=90°+90°=180°,
∴∠O+∠EPF=180°,即∠O+∠EPA+∠HPA+∠HPB+∠FPB=180°.
∵PE=PH,PA=PA,PE⊥AC,PH⊥AB,
∴△PEA≌△PHA(HL),
∴∠EPA=∠HPA. 同理,∠FPB=∠HPB,
∴∠O+2(∠HPA+∠HPB)=180°, 即∠O+2∠APB=180°,
∴∠APB=90°−$\frac{1}{2}$∠O.
∴③错误.故选C;

6. 教材P38例2·变式 如图,O是△ABC的三条角平分线的交点,连接OA,OB,OC,若△OAB,△OBC,△OAC的面积分别为S1,S2,S3,则下列关系正确的是( ).

A.S1>S2+S3
B.S1=S2+S3
C.S1<S2+S3
D.无法确定
]

A.S1>S2+S3
B.S1=S2+S3
C.S1<S2+S3
D.无法确定
]
答案:
C [解析]如图,过点O作OD⊥AB于点D,OE⊥BC于点E,OF⊥AC于点F.
∵O是△ABC的三条角平分线的交点,
∴OD=OE=OF.
∵S1=$\frac{1}{2}$AB·OD,S2+S3=$\frac{1}{2}$BC·OE+$\frac{1}{2}$AC·OF=$\frac{1}{2}$OD·(BC+AC),又AB<BC+AC,
∴S1<S2+S3.故选C. 归纳总结 本题考查了角平分线的性质:角平分线上的点到角两边的距离相等、三角形的面积公式等知识,解题的关键是学会添加常用辅助线,学会利用面积法构建方程解决问题,属于中考常考题型.
C [解析]如图,过点O作OD⊥AB于点D,OE⊥BC于点E,OF⊥AC于点F.
∵O是△ABC的三条角平分线的交点,
∴OD=OE=OF.

∵S1=$\frac{1}{2}$AB·OD,S2+S3=$\frac{1}{2}$BC·OE+$\frac{1}{2}$AC·OF=$\frac{1}{2}$OD·(BC+AC),又AB<BC+AC,
∴S1<S2+S3.故选C. 归纳总结 本题考查了角平分线的性质:角平分线上的点到角两边的距离相等、三角形的面积公式等知识,解题的关键是学会添加常用辅助线,学会利用面积法构建方程解决问题,属于中考常考题型.
7.(2024·盐城大丰区期中)如图,点P是∠ACB的平分线CD上一点,PE⊥BC于点E,点F为射线CA上一点. 若PE= 6,则PF长的最小值是(
A.4
B.5.5
C.6
D.8
]
C
).A.4
B.5.5
C.6
D.8
]
答案:
C [解析]
∵点P是∠ACB的平分线CD上一点,PE⊥BC于点E,PE=6, 当PF⊥AC时,PF最短=PE=6. 垂线段最短 故选C; 归纳总结 本题考查的是角平分线的性质,熟知角的平分线上的点到角两边的距离相等是解答此题的关键
∵点P是∠ACB的平分线CD上一点,PE⊥BC于点E,PE=6, 当PF⊥AC时,PF最短=PE=6. 垂线段最短 故选C; 归纳总结 本题考查的是角平分线的性质,熟知角的平分线上的点到角两边的距离相等是解答此题的关键
8. 若△ABC的周长为41 cm,边BC= 17 cm,且AB<AC,角平分线AD将△ABC的面积分成3∶5的两部分,则AB等于______cm.
答案:
9 [解析]如图,过点D作DE⊥AB于点E,DF⊥AC于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵AD将△ABC分为面积比为3:5的两部分,
∴AB:AC=3:5. 又△ABC的周长为41cm,BC=17cm,
∴AB+AC=41−17=24(cm). 设AB=3xcm,AC=5xcm,则3x+5x=24, 解得x=3,则AB=3x=9cm.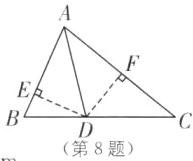
9 [解析]如图,过点D作DE⊥AB于点E,DF⊥AC于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵AD将△ABC分为面积比为3:5的两部分,
∴AB:AC=3:5. 又△ABC的周长为41cm,BC=17cm,
∴AB+AC=41−17=24(cm). 设AB=3xcm,AC=5xcm,则3x+5x=24, 解得x=3,则AB=3x=9cm.

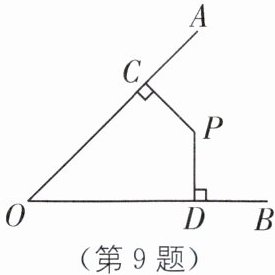
9. 教材P37问题2·变式(2025·南京联合体期中)证明:角的内部到角两边距离相等的点在角的平分线上.
已知:如图,点P在∠AOB内,______,______,______.
求证:______.
证明:
]
已知:如图,点P在∠AOB内,______,______,______.
求证:______.
证明:
]

答案:
已知:PC⊥OA于点C,PD⊥OB于点D,PC=PD;求证:点P在∠AOB的平分线上.证明:如图,连接OP,
∵PC⊥OA,PD⊥OB,
∴∠OCP=∠ODP=90°. 在Rt△POC和Rt△POD中,{PC=PD,PO=PO},
在Rt△POC和Rt△POD中,{PC=PD,PO=PO},
∴Rt△POC≌Rt△POD(HL),
∴∠COP=∠DOP,
∴点P在∠AOB的平分线上. 归纳总结 本题主要考查了全等三角形的判定和性质、垂直的定义,熟练掌握全等三角形的判定和性质,理解角平分线的定义、垂直的定义是解决问题的关键
已知:PC⊥OA于点C,PD⊥OB于点D,PC=PD;求证:点P在∠AOB的平分线上.证明:如图,连接OP,
∵PC⊥OA,PD⊥OB,
∴∠OCP=∠ODP=90°.
 在Rt△POC和Rt△POD中,{PC=PD,PO=PO},
在Rt△POC和Rt△POD中,{PC=PD,PO=PO},∴Rt△POC≌Rt△POD(HL),
∴∠COP=∠DOP,
∴点P在∠AOB的平分线上. 归纳总结 本题主要考查了全等三角形的判定和性质、垂直的定义,熟练掌握全等三角形的判定和性质,理解角平分线的定义、垂直的定义是解决问题的关键
查看更多完整答案,请扫码查看


