《2025年实验班提优训练八年级数学上册苏科版》

12. (2024·西宁中考)若长度分别为 3,6,a 的三条线段能组成一个三角形,则整数 a 的值可以是______.(写出一个即可)
4

答案： (答案不唯一)[解析]
∵长度分别为3,6,a的三条线段能组成一个三角形,
∴6-3＜a＜6+3,
∴3＜a＜9,
∴整数a的值可以是4(答案不唯一).

13. (2024·山东菏泽期末)下列长度的三条线段,能组成三角形的是______.(填序号)
①1,2,3；②2,3,4；③1,4,2；④6,2,3.
②

答案： ② [解析]①1+2=3,长度是1,2,3的线段不能组成三角形.故①不符合题意；
②2+3＞4,长度是2,3,4的线段能组成三角形.故②符合题意；
③1+2＜4,长度是1,2,4的线段不能组成三角形.故③不符合题意；
④2+3＜6,长度是2,3,6的线段不能组成三角形.故④不符合题意.

14. (2025·江西南昌东湖区期中)已知△ABC 的三边长是 a,b,c.
(1)若 a= 6,b= 8,且三角形的周长是小于 22 的偶数,求 c 的值；
(2)化简|a+b-c|+|c-a-b|.

答案：
(1)
∵a,b,c是△ABC的三边,a=6,b=8,
∴2＜c＜14.
∵三角形的周长是小于22的偶数,
∴2＜c＜8,
∴c=4或6；
(2)|a+b-c|+|c-a-b|=a+b-c+c+a+b=2a+2b-2c.

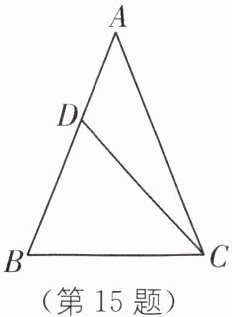
15. 如图,在△ABC 中,AB= AC,D 是边 AB 上一点.
(1)通过度量 AB,CD,DB 的长度,确定 AB 与$\frac{1}{2}(CD+DB)$的大小关系；
(2)试用你所学的知识来说明这个不等关系是成立的.

]

答案：
(1)AB＞$\frac{1}{2}(CD+DB)$；
(2)
∵在△ADC中,AD+AC＞CD,
∴(AD+DB)+AC＞CD+DB,即AB+AC＞CD+DB.又AB=AC,
∴2AB＞CD+DB,
∴AB＞$\frac{1}{2}(CD+DB)$.

16. 分类讨论思想 若三边均不相等的三角形的三边 a,b,c 满足 a-b＞b-c(a 为最长边,c 为最短边),则称它为“不均衡三角形”.例如,一个三角形三边分别为 7,5,4,因为 7-5＞5-4,所以这个三角形为“不均衡三角形”.
(1)以下 4 组长度的小木棍能组成“不均衡三角形”的为②.(填序号)
①4 cm,2 cm,1 cm；②13 cm,18 cm,9 cm；③19 cm,20 cm,19 cm；④9 cm,8 cm,6 cm.
(2)已知“不均衡三角形”三边分别为 2x+2,16,2x-6,直接写出 x 的整数值为10或12或13或14.

答案：
(1)②；
(2)10或12或13或14 [解析]①当16为最长边长时,由题意,得16-(2x+2)＞2x+2-(2x-6),解得x＜3.
∵2x-6＞0,
∴x＞3.故互相矛盾,舍去；
②当16为中间边长时,由题意,得2x+2＞16＞2x-6,解得7＜x＜11.又2x+2-16＞16-(2x-6),解得x＞9,
∴9＜x＜11.
∵x为整数,
∴x=10.经检验,当x=10时,22,16,14可以构成三角形；
③当16为最短边长时,由题意,得2x-6＞16,解得x＞11.
∵2x+2-(2x-6)＞2x-6-16,解得x＜15,
∴11＜x＜15.
∵x为整数,
∴x=12或13或14.经检验,x=12,13,14时都可以构成三角形.综上所述,x的整数值为10或12或13或14.

17. 转化思想 将 a 克糖放入水中,得到 b 克糖水,此时糖水的浓度为$\frac{a}{b}(b＞a＞0). (1)$再往杯中加入 m(m＞0)克糖,生活经验告诉我们糖水变甜了,用数学关系式可以表示为$\frac{a+m}{b+m}＞\frac{a}{b}$；
(2)请证明(1)中的数学关系式；
(3)在△ABC 中,三条边的长度分别为 a,b,c,证明$:\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}＜2.$

证明：(2)利用作差法比较大小：$\frac{a+m}{b+m}-\frac{a}{b}=\frac{b(a+m)}{b(b+m)}-\frac{a(b+m)}{b(b+m)}=\frac{bm-am}{b(b+m)}=\frac{m(b-a)}{b(b+m)}$.
∵m＞0，b＞a＞0，
∴b-a＞0，b+m＞0，即$\frac{m(b-a)}{b(b+m)}＞0$，
∴$\frac{a+m}{b+m}-\frac{a}{b}＞0$，即$\frac{a+m}{b+m}＞\frac{a}{b}$.
(3)在△ABC中，a+b＞c，b+c＞a，c+a＞b，且a＞0，b＞0，c＞0，
∴$\frac{a}{b+c}＜1$，$\frac{b}{c+a}＜1$，$\frac{c}{a+b}＜1$.由糖水不等式可得$\frac{a}{b+c}＜\frac{a+a}{b+c+a}$，$\frac{b}{c+a}＜\frac{b+b}{c+a+b}$，$\frac{c}{b+a}＜\frac{c+c}{a+b+c}$，
∴$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}＜\frac{a+a}{b+c+a}+\frac{b+b}{c+a+b}+\frac{c+c}{a+b+c}=2$，
∴$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}＜2$.

答案：
(1)$\frac{a+m}{b+m}$＞$\frac{a}{b}$ [解析]由题意知,加入m克糖后糖水浓度为$\frac{a+m}{b+m}$,由糖水变甜可得$\frac{a+m}{b+m}$＞$\frac{a}{b}$；
(2)利用作差法比较大小:$\frac{a+m}{b+m}$-$\frac{a}{b}$=$\frac{b(a+m)}{b(b+m)}$-$\frac{a(b+m)}{b(b+m)}$=$\frac{bm-am}{b(b+m)}$=$\frac{m(b-a)}{b(b+m)}$.
∵m＞0,b＞a＞0,
∴b-a＞0,b+m＞0,即$\frac{m(b-a)}{b(b+m)}$＞0,
∴$\frac{a+m}{b+m}$-$\frac{a}{b}$＞0,即$\frac{a+m}{b+m}$＞$\frac{a}{b}$；
(3)在△ABC中,a+b＞c,b+c＞a,c+a＞b,且a＞0,b＞0,c＞0,
∴$\frac{a}{b+c}$＜1,$\frac{b}{c+a}$＜1,$\frac{c}{a+b}$＜1.由糖水不等式可得$\frac{a}{b+c}$＜$\frac{a+a}{b+c+a}$,$\frac{b}{c+a}$＜$\frac{b+b}{c+a+b}$,$\frac{c}{b+a}$＜$\frac{c+c}{a+b+c}$,
∴$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$＜$\frac{a+a}{b+c+a}$+$\frac{b+b}{c+a+b}$+$\frac{c+c}{a+b+c}$=2,
∴$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$＜2.