《2025年实验班提优训练八年级数学上册苏科版》

1. 已知直角三角形的面积为 $6\ cm^2$,两直角边的差为 $1\ cm$,则它的斜边长为5cm.

答案： 5 [解析]设两直角边长分别为a cm,b cm(a＞b＞0)，
∵直角三角形的面积为6 cm²，
∴$\frac{1}{2}ab = 6$，即ab = 12。又两直角边的差为1 cm，
∴a - b = 1，
∴$a^{2}+b^{2}=(a - b)^{2}+2ab = 1 + 24 = 25$，
∴它的斜边长为5 cm。

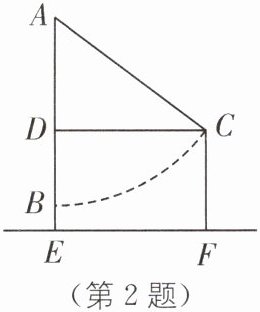
2. 新情境 荡秋千 如图,秋千静止时,踏板离地的垂直高度 $BE= 1\ m$,将它往前推 $6\ m$ 至 $C$ 处时(即水平距离 $CD= 6\ m$),踏板离地的垂直高度 $CF= 4\ m$,它的绳索始终拉直,则绳索 $AC$ 的长是(B).

A.$\frac{21}{2}\ m$
B.$\frac{15}{2}\ m$
C.$6\ m$
D.$\frac{9}{2}\ m$

答案： B [解析]设绳长为x m，在Rt△ADC中，AD = AB - BD = AB - (DE - BE)=x - (4 - 1)=(x - 3)m，DC = 6 m，AC = x m，
∴$AD^{2}+DC^{2}=AC^{2}$，根据题意可得$x^{2}=(x - 3)^{2}+6^{2}$，解得$x=\frac{15}{2}$，
∴绳索AC的长是$\frac{15}{2}$m。故选B。

3. 传统文化 《数书九章》 (2025·无锡期末)我国南宋数学家秦九韶的著作《数书九章》中有一道问题:“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步,欲知为田几何?”问题大意:如图,在 $\triangle ABC$ 中,$AB= 13$ 里,$BC= 14$ 里,$AC= 15$ 里,则 $\triangle ABC$ 的面积是( ).

答案：
C [解析]如图，过点A作AD⊥BC于点D，

设BD = x里，则CD = (14 - x)里，在Rt△ABD中，$AD^{2}+x^{2}=13^{2}$，在Rt△ADC中，$AD^{2}=15^{2}-(14 - x)^{2}$，
∴$13^{2}-x^{2}=15^{2}-(14 - x)^{2}$，解得x = 5。在Rt△ABD中，$AD=\sqrt{13^{2}-5^{2}} = 12$(里)，
∴△ABC的面积=$\frac{1}{2}BC\cdot AD=\frac{1}{2}×14×12 = 84$(平方里)。故选C。

4. 如图是矗立在高速公路水平地面上的交通警示牌,$CM \perp MB$,经测量得到如下数据:$AM= 4\ m$,$AB= 4\ m$,$\angle MAD= 45^\circ$,$CM:CB= 3:5$,则警示牌的高 $CD$ 为2m.

答案： 2

5. 如图,在 $Rt\triangle ABC$ 中,$\angle ACB= 90^\circ$,$AB= \sqrt{6}\ cm$,$AC= \sqrt{2}\ cm$,点 $P$ 在线段 $BC$ 上,当 $AP= BP$ 时,$AP$ 的长度为$\frac{3}{2}$cm.

答案： $\frac{3}{2}$

6. 在 $Rt\triangle ABC$ 中,$\angle ACB= 90^\circ$,$AC= 4$,$BC= 8$,动点 $P$ 在射线 $BC$ 上移动,连接 $AP$.如果 $\angle APC= 2\angle B$,则线段 $BP$ 的长为5或11.

答案： 5或11

7. 如图,四边形 $ABCD$ 是边长为 $9$ 的正方形纸片,将其沿 $MN$ 折叠,使点 $B$ 落在 $CD$ 边上的 $B'$处,点 $A$ 的对应点为 $A'$,且 $B'C= 3$,则 $AM$ 的长是______2.

答案： 2 [解析]设AM = x，连接BM，MB'，由题意知，MB = MB'，则有$AB^{2}+AM^{2}=BM^{2}=B'M^{2}=MD^{2}+DB'^{2}$，即$9^{2}+x^{2}=(9 - x)^{2}+(9 - 3)^{2}$，解得x = 2，即AM = 2。

8. (2025·河北石家庄裕华区期中)如图,一架无人机悬停在空中点 $A$ 处,点 $A$ 与地面上点 $B$ 之间的距离 $AB= 20$ 米,点 $A$ 与地面上点 $C$(点 $B,C$ 处于同一水平面上)的距离 $AC= 25$ 米,且 $BC= 15$ 米.
(1)求 $\angle ABC$ 的度数;
(2)现这架无人机沿 $AB$ 所在直线向下飞行至点 $D$ 处,若点 $D$ 恰好在边 $AC$ 的垂直平分线上,连接 $CD$,求这架无人机向下飞行的距离($AD$ 的长).

答案：
(1)
∵$AB^{2}+BC^{2}=20^{2}+15^{2}=625$，$AC^{2}=25^{2}=625$，
∴$AB^{2}+BC^{2}=AC^{2}$，
∴△ABC是直角三角形，∠ABC = 90°。
(2)设AD = x米，若点D恰好在边AC的垂直平分线上，则CD = AD = x米，BD = (20 - x)米，在Rt△BDC中，$DC^{2}=BD^{2}+BC^{2}$，
∴$x^{2}=(20 - x)^{2}+15^{2}$，解得$x=\frac{125}{8}$。故这架无人机向下飞行的距离(AD的长)为$\frac{125}{8}$米。