第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
9. 在 $\triangle ABC$ 中,$AB= 15$,$AC= 13$,高 $AD= 12$,则 $\triangle ABC$ 的周长为(
A.32
B.42
C.32 或 42
D.38 或 42
C
).A.32
B.42
C.32 或 42
D.38 或 42
答案:
C
10. 在 $Rt\triangle ABC$ 中,$\angle C= 90^\circ$,$AC= 6$,$BC= 8$,将它其中一个锐角沿着某条直线翻折,使该锐角顶点落在其对边的中点 $D$,折痕交另一个直角边于点 $E$,交斜边于 $F$,则 $DE$ 的长为
$\frac{73}{16}$或$\frac{13}{3}$
.
答案:
$\frac{73}{16}$或$\frac{13}{3}$
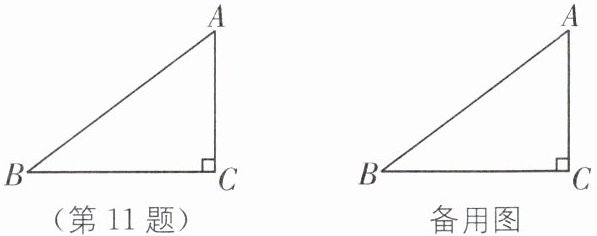
11. 如图,在 $\triangle ABC$ 中,$\angle ACB= 90^\circ$,$AB= 5\ cm$,$BC= 4\ cm$,若点 $P$ 从点 $A$ 出发,以每秒 $2\ cm$ 的速度沿折线 $A-B-C-A$ 运动,设运动时间为 $t$ 秒($t>0$).
(1)若点 $P$ 在 $BC$ 上,且满足 $PA= PB$,求此时 $t$ 的值;
(2)若点 $P$ 恰好在 $\angle ABC$ 的平分线上,求此时 $t$ 的值;
(3)在点 $P$ 运动过程中,当 $t$ 为何值时,$\triangle ACP$ 为等腰三角形.
(1)若点 $P$ 在 $BC$ 上,且满足 $PA= PB$,求此时 $t$ 的值;
(2)若点 $P$ 恰好在 $\angle ABC$ 的平分线上,求此时 $t$ 的值;
(3)在点 $P$ 运动过程中,当 $t$ 为何值时,$\triangle ACP$ 为等腰三角形.

答案:
(1)如图
(1),设PB = PA = x cm,则PC = (4 - x)cm,
∵∠ACB = 90°,AB = 5 cm,BC = 4 cm,
∴AC = 3 cm。在Rt△ACP中,$AC^{2}+PC^{2}=AP^{2}$,
∴$3^{2}+(4 - x)^{2}=x^{2}$,解得$x=\frac{25}{8}$,
∴$BP=\frac{25}{8}$cm,
∴$t=\frac{AB + BP}{2}=\frac{5+\frac{25}{8}}{2}=\frac{65}{16}$。
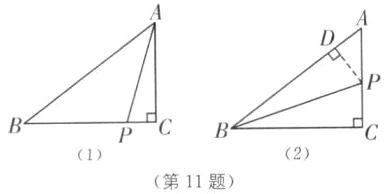
(2)如图
(2),过点P作PD⊥AB于点D。
∵BP平分∠ABC,∠C = 90°,
∴PD = PC。
∵BP = BP,
∴Rt△BPD≌Rt△BPC(HL),
∴BC = BD = 4 cm,
∴AD = 5 - 4 = 1(cm)。设PD = PC = y cm,则AP = (3 - y)cm,在Rt△ADP中,$AD^{2}+PD^{2}=AP^{2}$,
∴$1^{2}+y^{2}=(3 - y)^{2}$,解得$y=\frac{4}{3}$,
∴$CP=\frac{4}{3}$cm,
∴$t=\frac{AB + BC + CP}{2}=\frac{5 + 4+\frac{4}{3}}{2}=\frac{31}{6}$;当点P与点B重合时,点P也在∠ABC的平分线上,此时,$t=\frac{AB}{2}=\frac{5}{2}$。综上所述,点P恰好在∠ABC的平分线上时,t的值为$\frac{31}{6}$或$\frac{5}{2}$。
(3)分四种情况:
①如图
(3),当P在AB上,且AP = CP时,

∠A = ∠ACP,而∠A + ∠B = 90°,∠ACP + ∠BCP = 90°,
∴∠B = ∠BCP,
∴CP = BP,
∴P是AB的中点,即$AP=\frac{1}{2}AB=\frac{5}{2}$cm,
∴$t=\frac{AP}{2}=\frac{5}{4}$;
②如图
(4),当P在AB上且AP = CA = 3 cm时,$t=\frac{AP}{2}=\frac{3}{2}$;
③如图
(5),当P在AB上且AC = PC时,过点C作CD⊥AB于点D,则$CD=\frac{AC\cdot BC}{AB}=\frac{12}{5}$cm,

∴在Rt△ACD中,$AD=\frac{9}{5}$cm,
∴$AP = 2AD=\frac{18}{5}$cm,
∴$t=\frac{AP}{2}=\frac{9}{5}$;
④如图
(6),当P在BC上且AC = PC = 3 cm时,BP = 4 - 3 = 1(cm),
∴$t=\frac{AB + BP}{2}=\frac{6}{2}=3$。
综上所述,当$t=\frac{5}{4}$或$\frac{3}{2}$或$\frac{9}{5}$或3时,△ACP为等腰三角形。
(1)如图
(1),设PB = PA = x cm,则PC = (4 - x)cm,
∵∠ACB = 90°,AB = 5 cm,BC = 4 cm,
∴AC = 3 cm。在Rt△ACP中,$AC^{2}+PC^{2}=AP^{2}$,
∴$3^{2}+(4 - x)^{2}=x^{2}$,解得$x=\frac{25}{8}$,
∴$BP=\frac{25}{8}$cm,
∴$t=\frac{AB + BP}{2}=\frac{5+\frac{25}{8}}{2}=\frac{65}{16}$。

(2)如图
(2),过点P作PD⊥AB于点D。
∵BP平分∠ABC,∠C = 90°,
∴PD = PC。
∵BP = BP,
∴Rt△BPD≌Rt△BPC(HL),
∴BC = BD = 4 cm,
∴AD = 5 - 4 = 1(cm)。设PD = PC = y cm,则AP = (3 - y)cm,在Rt△ADP中,$AD^{2}+PD^{2}=AP^{2}$,
∴$1^{2}+y^{2}=(3 - y)^{2}$,解得$y=\frac{4}{3}$,
∴$CP=\frac{4}{3}$cm,
∴$t=\frac{AB + BC + CP}{2}=\frac{5 + 4+\frac{4}{3}}{2}=\frac{31}{6}$;当点P与点B重合时,点P也在∠ABC的平分线上,此时,$t=\frac{AB}{2}=\frac{5}{2}$。综上所述,点P恰好在∠ABC的平分线上时,t的值为$\frac{31}{6}$或$\frac{5}{2}$。
(3)分四种情况:
①如图
(3),当P在AB上,且AP = CP时,

∠A = ∠ACP,而∠A + ∠B = 90°,∠ACP + ∠BCP = 90°,
∴∠B = ∠BCP,
∴CP = BP,
∴P是AB的中点,即$AP=\frac{1}{2}AB=\frac{5}{2}$cm,
∴$t=\frac{AP}{2}=\frac{5}{4}$;
②如图
(4),当P在AB上且AP = CA = 3 cm时,$t=\frac{AP}{2}=\frac{3}{2}$;
③如图
(5),当P在AB上且AC = PC时,过点C作CD⊥AB于点D,则$CD=\frac{AC\cdot BC}{AB}=\frac{12}{5}$cm,

∴在Rt△ACD中,$AD=\frac{9}{5}$cm,
∴$AP = 2AD=\frac{18}{5}$cm,
∴$t=\frac{AP}{2}=\frac{9}{5}$;
④如图
(6),当P在BC上且AC = PC = 3 cm时,BP = 4 - 3 = 1(cm),
∴$t=\frac{AB + BP}{2}=\frac{6}{2}=3$。
综上所述,当$t=\frac{5}{4}$或$\frac{3}{2}$或$\frac{9}{5}$或3时,△ACP为等腰三角形。
12. 如图,在 $\triangle ABC$ 中,$CE$ 平分 $\angle ACB$,$CF$ 平分 $\triangle ABC$ 的外角 $\angle ACD$,且 $EF // BC$ 交 $AC$ 于 $M$,若 $CM= 4$,则 $CE^2+CF^2$ 的值为(

A.8
B.16
C.32
D.64
D
).
A.8
B.16
C.32
D.64
答案:
D
13. (2025·南京金陵中学河西分校期中)如图,在 $Rt\triangle ABC$ 中,$\angle ACB= 90^\circ$,$AC= 2$,$BC= 4$.分别以 $AB$,$AC$,$BC$ 为边在 $AB$ 的同侧作正方形 $ABEF$,$ACPQ$,$BCMN$,四块阴影部分的面积分别为 $S_1$,$S_2$,$S_3$,$S_4$,则 $S_1+S_2+S_3+S_4$ 等于(
A.12
B.14
C.16
D.18
A
).A.12
B.14
C.16
D.18
答案:
A
14. 对角线互相垂直的四边形叫作“垂美”四边形,现有如图所示的“垂美”四边形 $ABCD$,对角线 $AC$,$BD$ 交于点 $O$,若 $AD= 3$,$BC= 8$,则 $AB^2+CD^2= $
73
.
答案:
73 [解析]
∵BD⊥AC,
∴∠COB = ∠AOB = ∠AOD = ∠COD = 90°。在Rt△COB和Rt△AOD中,根据勾股定理,得$BO^{2}+CO^{2}=CB^{2}$,$OD^{2}+OA^{2}=AD^{2}$,
∴$CB^{2}+AD^{2}=BO^{2}+CO^{2}+OD^{2}+OA^{2}=64 + 9 = 73$。
∵$AB^{2}=BO^{2}+AO^{2}$,$CD^{2}=OC^{2}+OD^{2}$,
∴$AB^{2}+CD^{2}=BO^{2}+AO^{2}+OC^{2}+OD^{2}=(BO^{2}+OC^{2})+(AO^{2}+OD^{2})=CB^{2}+AD^{2}=73$。
∵BD⊥AC,
∴∠COB = ∠AOB = ∠AOD = ∠COD = 90°。在Rt△COB和Rt△AOD中,根据勾股定理,得$BO^{2}+CO^{2}=CB^{2}$,$OD^{2}+OA^{2}=AD^{2}$,
∴$CB^{2}+AD^{2}=BO^{2}+CO^{2}+OD^{2}+OA^{2}=64 + 9 = 73$。
∵$AB^{2}=BO^{2}+AO^{2}$,$CD^{2}=OC^{2}+OD^{2}$,
∴$AB^{2}+CD^{2}=BO^{2}+AO^{2}+OC^{2}+OD^{2}=(BO^{2}+OC^{2})+(AO^{2}+OD^{2})=CB^{2}+AD^{2}=73$。
15. 如图,四边形 $ABCD$ 和四边形 $AEFG$ 都是正方形,点 $B$ 在 $EF$ 上,$S_1= 140$,$S_2= 124$,求 $EB$ 的长.


答案:
设△ABE的面积为S,
∵$S_{正方形ABCD}=S + S_{1}=S + 140$,$S_{正方形AEFG}=S + S_{2}=S + 124$,而$S_{正方形ABCD}=AB^{2}$,$S_{正方形AEFG}=AE^{2}$,
∴$AB^{2}-AE^{2}=140 - 124 = 16$。在Rt△ABE中,$BE^{2}=AB^{2}-AE^{2}=16$,
∴BE = 4。
∵$S_{正方形ABCD}=S + S_{1}=S + 140$,$S_{正方形AEFG}=S + S_{2}=S + 124$,而$S_{正方形ABCD}=AB^{2}$,$S_{正方形AEFG}=AE^{2}$,
∴$AB^{2}-AE^{2}=140 - 124 = 16$。在Rt△ABE中,$BE^{2}=AB^{2}-AE^{2}=16$,
∴BE = 4。
查看更多完整答案,请扫码查看


