《2025年实验班提优训练八年级数学上册苏科版》

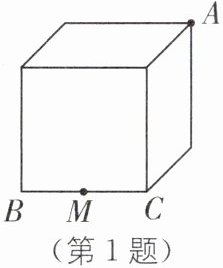
1. 如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从M点沿盒子的表面爬行到A点的最短距离为( ).

A.$\sqrt{12}$
B.$\sqrt{13}$
C.$\sqrt{14}$
D.$\sqrt{17}$

答案：
1.B　[解析]如图,蚂蚁沿路线AM爬行路程最短，
　　　　　　　　
∵BC=2,M为BC的中点，
∴MD=3,AD=2,
∴AM=√(3²+2²)=√13.故选B

2. 如图是一块长、宽、高分别是6 cm,4 cm 和3 cm 的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是(C).
A.$(3+\sqrt{52})$ cm
B.$\sqrt{97}$ cm
C.$\sqrt{85}$ cm
D.$\sqrt{109}$ cm

答案： 2.C

3. 如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC= 6,点P移动的最短距离为5,求圆柱的底面周长.

答案：
3.如图，连接AS,
　　　　　　　
　在圆柱的侧面展开图ABCD中,BC=6,BC⊥AB，
∵点P移动的最短距离为5,
∴AS=5.
∵点S是BC的中点，
∴BS=1/2BC=1/2×6=3,
∴AB=√(AS² - BS²)=√(5² - 3²)=4,
∴圆柱的底面周长为2AB=2×4=8.

4. 如图,某国道通过A,B两个村庄,而C村庄离国道较远,为了响应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道,已知C村到A,B两村的距离分别为6 km,8 km,A,B两村的距离为10 km,那么这条水泥路的最短距离为多少？

答案：
4.如图，过点C作CD⊥AB，垂足为D,则这条水泥路的最短距离为CD的长度，
　　　　　　　　
　在△ABC中,AC=6km,BC=8km,AB=10km,
　则6²+8²=10²,即AC²+BC²=AB²,
∴△ABC为直角三角形.
∵S△ABC=1/2AB·CD=1/2AC·BC,
∴CD=(AC·BC)/AB=(6×8)/10=4.8(km),
∴这条水泥路的最短距离为4.8km.

5. 如图,河CD的同侧有A,B两个村,且AB= $\sqrt{52}$ km,A,B两村到河的距离分别为AC= 2 km,BD= 6 km. 现要在河边CD上建一水厂分别向A,B两村输送自来水,铺设水管的工程费每千米需2000元. 请你在河岸CD上选择水厂位置O,使铺设水管的总费用最省,并求出铺设水管的总费用.

答案：
5.如图,作点A关于CD的对称点A',连接BA'交CD于O,点O即为水厂的位置,AO=A'O,AO+OB=A'O+OB=A'B.
过点A'作A'E//CD交BD的延长线于点E,过点A作AF ⊥BD于点F,

则AF=A'E,DF=AC=2km,DE=A'C=2km.
∴BF=BD - FD=6 - 2=4(km).
在Rt△ABF中,AF²=AB² - BF²=(√52)² - 4²=36,
∴AF=6km,
∴A'E=6km.
在Rt△A'BE中,BE=BD+DE=8km,
由勾股定理得A'B=√(A'E²+BE²)=√(6²+8²)=10(km).
∴铺设水管总费用为2000×10=20000(元).故铺设水管的总费用为20000元.