《2025年实验班提优训练八年级数学上册苏科版》

9. 在△ABC中,已知AB= 10,AC= 17,边BC上的高AD= 8,求BC的长.

答案：
如图
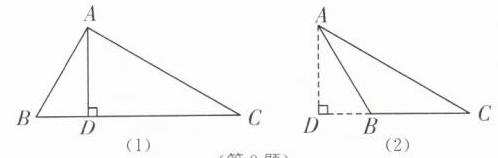
(1)，当高在三角形内部时，在Rt△ABD中,由勾股定理,得BD²=AB² - AD²=10² - 8²=36,所以BD=6.在Rt△ACD中,由勾股定理,得CD²=AC² - AD²=17² - 8²=225,所以CD=15.所以BC=BD+CD=6+15=21;
如图
(2),当高在三角形外部时,在Rt△ABD中,由勾股定理,得BD²=AB² - AD²=10² - 8²=36,所以BD=6.在Rt△ACD中,由勾股定理,得CD²=AC² - AD²=17² - 8²=225,所以CD=15.所以BC=CD - BD=15 - 6=9.故BC的长为21或9.

10. 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC= CD.

(1)求证：△BCE≌△DCF；
(2)若AB= 21,AD= 9,BC= CD= 10,求AC的长.

答案：
(1)
∵AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,
∴∠CEB=∠CFD=90°,CE=CF.又BC=DC,
∴Rt△BCE≌Rt△DCF(HL).
(2)由
(1),得Rt△BCE≌Rt△DCF,
∴DF=BE.设DF=BE=x,
∵∠CFA=∠CEA=90°,CF=CE,AC=AC,
∴Rt△AFC≌Rt△AEC(HL),
∴AF=AE,即AD+DF=AB - BE.
∵AB=21,AD=9,DF=BE=x,
∴9+x=21 - x,解得x=6.在Rt△DCF中,
∵DF=6,CD=10,
∴CF=8.在Rt△AFC中,AC²=CF²+AF²=8²+(9+6)²=289,
∴AC=17.故AC的长为17.

11. 中考新考法 探究不同条件下线段数量关系 如图,在△ABC中,AB= AC.
(1)若P为BC的中点,求证：$AB^2-AP^2= PB·PC；$
(2)若P为BC上的任意一点,判断(1)中的结论是否成立,请证明；
(3)若P为BC延长线上一点,探究AB,AP,PB,PC之间的数量关系.
精选题解

答案：
(1)如图
(1),连接AP.
∵AB=AC,P是BC的中点，
∴AP⊥BC,PB=PC.在Rt△ABP中,AB²=BP²+AP²,
∴AB² - AP²=BP².又PB=PC,
∴PB·PC=BP²,
∴AB² - AP²=PB·PC.
(2)结论成立.证明如下:如图
(2),连接AP,过点A作AD⊥BC交BC于点D.
∵AB=AC,AD⊥BC,
∴BD=CD.在Rt△ABD中,AB²=AD²+BD²,同理AP²=AD²+DP²,
∴AB² - AP²=AD²+BD² - (AD²+DP²)=BD² - DP².又PB=BD+DP,PC=CD - DP=BD - DP,
∴PB·PC=(BD+DP)(BD - DP)=BD² - DP²,
∴AB² - AP²=PB·PC.
(3)AP² - AB²=PB·PC.理由如下:如图
(3),连接AP,过点A作AD⊥BC交BC于点D.
∵AB=AC,AD⊥BC,
∴BD=CD.在Rt△ABD中,AB²=AD²+BD²,在Rt△ADP中,AP²=AD²+DP²,
∴AP² - AB²=(AD²+DP²) - (AD²+BD²)=DP² - BD².又PB=DP+BD,PC=DP - CD=DP - BD,
∴PB·PC=(DP+BD)(DP - BD)=DP² - BD²,
∴AP² - AB²=PB·PC.

12. 传统文化 赵爽弦图 (2024·南通中考)“赵爽弦图”巧妙利用面积关系证明了勾股定理. 如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形. 设直角三角形的两条直角边长分别为m,n(m＞n). 若小正方形面积为5,$(m+n)^2= 21$,则大正方形面积为(B).

A.12
B.13
C.14
D.15

答案： B　[解析]由题意可知,中间小正方形的边长为m - n,
∴(m - n)²=5,即m²+n² - 2mn=5.①
∵(m + n)²=21,
∴m²+n²+2mn=21,②由①+②,得2(m²+n²)=26,
∴大正方形的面积为m²+n²=13.故选B.