《2025年实验班提优训练八年级数学上册苏科版》

1. (2023·扬州中考)已知$a= \sqrt{5}$,$b= 2$,$c= \sqrt{3}$,则$a$,$b$,$c$的大小关系是(C).
A.$b＞a＞c$
B.$a＞c＞b$
C.$a＞b＞c$
D.$b＞c＞a$

答案： 1.C 解析
∵3＜4＜5,
∴√3＜√4＜√5,即√3＜2＜√5,
∴a＞b＞c.故选C.
知识拓展 本题考查了实数的大小比较法则,能熟记实数的大小比较法则是解题的关键,注意:任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数比大小,绝对值大的反而小.

2. 比较$\sqrt{m-5}和\sqrt[3]{4-m}$的大小.

答案： 2.根据平方根的定义,可知m-5≥0,即m≥5,则4-m＜0,$\sqrt[3]{4-m}$＜0.又√m-5≥0,
∴√m-5＞$\sqrt[3]{4-m}$.

3. (2025·镇江句容期中)已知$a$为有理数,$A= 2a^2 - a - 6$,$B= a^2 - a - 10$,则$A$,$B$的大小关系是(A).
A.$A＞B$
B.$A= B$
C.$A＜B$
D.$A\geq B$

答案： 3.A 解析
∵A=2a²-a-6,B=a²-a-10,
∴A-B=(2a²-a-6)-(a²-a-10)=2a²-a-6-a²+a+10=a²+4＞0,
∴A＞B.故选A.

4. 实验班原创 比较$\frac{\sqrt{3}-1}{6}与\frac{1}{6}$的大小.

答案： 4.
∵$\frac{\sqrt{3}-1}{6}÷\frac{1}{6}=\sqrt{3}-1＜1$,
∴$\frac{\sqrt{3}-1}{6}＜\frac{1}{6}$.

5. 比较$\sqrt{2025}-\sqrt{2024}与\sqrt{2024}-\sqrt{2023}$的大小.

答案： 5.
∵$\frac{1}{\sqrt{2025}-\sqrt{2024}}=\sqrt{2025}+\sqrt{2024}$,→利用平方差公式变形即可得到$\frac{1}{\sqrt{2024}-\sqrt{2023}}=\sqrt{2024}+\sqrt{2023}$,且√2025+√2024＞√2024+√2023,
∴√2025-√2024＜√2024-√2023.

6. (2024·扬州仪征一模)比较大小:$\sqrt{5}-1$＜$\sqrt{3}$(填“＞”“＜”或“=”).

答案： 6.＜ 解析
∵√5-1＜2.5-1,2.5-1=1.5,
∴√5-1＜1.5.
∵√3＞1.5,
∴√5-1＜√3.

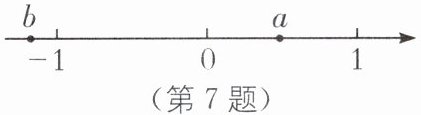
7. (2024·南通启东一模)实数$a$,$b$在数轴上的对应点的位置如图所示.把$a$,$b$,$-a$,$-b$按照从小到大的顺序排列,正确的是(D).

A. $b＜-a＜-b＜a$
B. $-a＜-b＜a＜b$
C. $-b＜a＜-a＜b$
D. $b＜-a＜a＜-b$

答案： 7.D 解析根据图示,可得0＜a＜1,b＜-1,
∴-1＜-a＜0,-b＞1,
∴b＜-a＜a＜-b.故选D.

8. (2025·北京丰台区一模)实数$a$,$b$,$c$在数轴上的对应点的位置如图所示,下列结论中正确的是(D).

A. $ac＞0$
B. $b+c＞0$
C. $|c|＞2$
D. $|c|＞|b|$

答案： 8.D

9. 比较$\sqrt{6}+2和\sqrt{57}-2$的大小.

答案： 9.
∵2＜√6＜3,7＜√57＜8,
∴√6+2＜3+2=5,√57-2＞7-2=5,
∴√6+2＜√57-2.