《2025年拔尖特训五年级数学上册苏教版》

(1)从一张底是 12 厘米、高是 8 厘米的平行四边形纸中剪下一个最大的三角形,这个三角形的面积是(48)平方厘米。

答案： 48

(2)一个三角形和一个平行四边形的高相等,面积也相等。若平行四边形的底是 12 分米,则三角形的底是(24)分米。

答案： 24

(3)如果一个平行四边形的底乘 6,高除以 2,那么这个平行四边形的面积扩大到原来的(3)倍。

答案： 3

(4)如图,平行四边形的周长是 80 cm,这个平行四边形的面积是300$cm^2。$

答案： 300　解析:先求平行四边形ABCD的边CD 的长，再求面积。

2. 在下面的方格纸上分别画一个平行四边形、一个三角形,使它们的面积都与图中长方形的面积相等。

答案：
答案不唯一,如　　

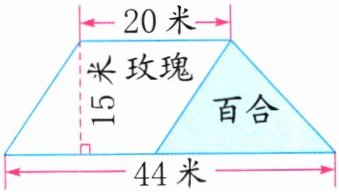
3. (生活应用)一个梯形花圃被分成了一个平行四边形和一个三角形,分别种了玫瑰和百合(如图)。玫瑰和百合各种了多少平方米？

答案： 玫瑰:20×15=300(平方米)
百合:(44−20)×15÷2=180(平方米)

(1)下面的梯形中,有( )组三角形的面积相等。


A.1
B.2
C.3
D.4

答案：
C　解析:如图，由等底等高的三角形面积相等可知，三角形ABC和三角形DBC、三角形ABD和三角形ACD的面积相等。因为三角形ABC和三角形DBC的面积相等，所以它们分别减去三角形BOC的面积后，所剩的面积相等，即三角形ABO和三角形DCO的面积相等,所以有3组三角形的面积相等。
　　　　　

(2)如图,有三个完全一样的平行四边形,涂色部分的面积相比,(D)。

A.甲最大
B.乙最大
C.丙最大
D.一样大

答案： D　解析:涂色部分的面积都等于平行四边形面积的一半。

5. (推理意识)如图,正方形的周长是 28 厘米,三角形 ABC 的面积是 17 平方厘米,求涂色部分的面积。

答案： 28÷4=7(厘米)　7×7−17=32(平方厘米)
解析:由题图可知，正方形与平行四边形等底等高，所以正方形的面积等于平行四边形的面积。又知正方形的周长是28厘米，可求出正方形的边长,再根据“正方形的面积=边长×边长”求出正方形的面积，即平行四边形的面积。因为平行四边形是由三角形ABC和涂色部分组成的，又已知三角形ABC的面积，所以用平行四边形的面积减去三角形ABC的面积就是涂色部分的面积。

6. 如图,P 是平行四边形 ABCD 外的一点,三角形 PAD 的面积是 20 平方分米,三角形 PBC 的面积是 45 平方分米。求平行四边形 ABCD 的面积。

答案：
45×2−20×2=50(平方分米)　解析:如图，过点P作AD的平行线，并分别与BA、CD的延长线相交于F、E两点，这样就得到了一个大平行四边形BCEF。观察可知，三角形PBC与平行四边形BCEF同底同高，则平行四边形BCEF的面积为45×2=90(平方分米);同理，平行四边形ADEF的面积为20×2=40(平方分米)。要求平行四边形ABCD的面积，只需用平行四边形BCEF的面积减去平行四边形ADEF的面积。