第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 计算下面图形的面积。
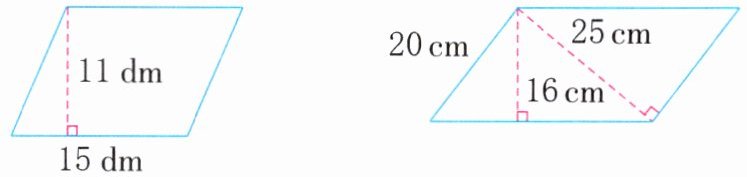
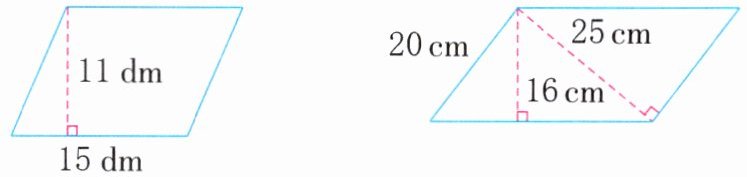
答案:
15×11=165(dm²) 20×25=500(cm²)
2. 在方格纸上画出两个形状不同,但面积都是16平方厘米的平行四边形。(每个小方格表示1平方厘米)


答案:
答案不唯一,如

答案不唯一,如

(1)如左下图,将一张平行四边形纸剪拼成一个长方形,周长
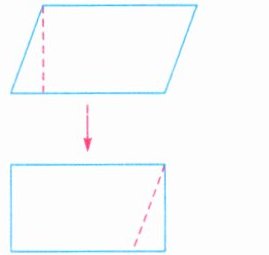
A.变大
B.变小
C.不变
D.无法确定
B
,面积C
。
A.变大
B.变小
C.不变
D.无法确定
答案:
BC
(2)如右上图,把一个平行四边形框架拉成长方形,周长
A.变大
B.变小
C.不变
D.无法确定
C
,面积A
。A.变大
B.变小
C.不变
D.无法确定
答案:
C A
(3)(几何直观)如图,长方形和平行四边形的面积相比,(
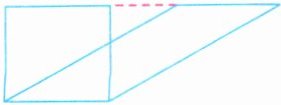
A.一样大
B.长方形的面积大
C.平行四边形的面积大
D.无法确定
A
)。
A.一样大
B.长方形的面积大
C.平行四边形的面积大
D.无法确定
答案:
A 解析:题图中长方形的长和平行四边形的底相同,长方形的宽和平行四边形的高相等,所以它们的面积一样大。
4. ★(1)如图,平行四边形一条底边上的高是5厘米,它的面积是多少平方厘米?
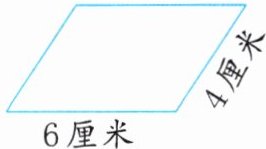
(2)一个平行四边形的两条高分别长10米、15米,它的一条底边长12米,求它的面积。

(2)一个平行四边形的两条高分别长10米、15米,它的一条底边长12米,求它的面积。
答案:
(1)4×5=20(平方厘米) 解析:由题图可知,6厘米的底边上的高不可能是5厘米,所以5厘米的高所对应的底为4厘米。根据“平行四边形的面积=底×高”计算即可。
(2)12×15=180(平方米) 解析:底边为12米,它所对应的高应为15米。
易错分析>>
忽略平行四边形中底与高的对应
因为直线外一点到这条直线的垂直线段最短,所以比高短的那条边是这条高对应的底。计算平行四边形的面积时,要正确选择数据,一定要用底乘所对应的高,可画图推理。
(1)4×5=20(平方厘米) 解析:由题图可知,6厘米的底边上的高不可能是5厘米,所以5厘米的高所对应的底为4厘米。根据“平行四边形的面积=底×高”计算即可。
(2)12×15=180(平方米) 解析:底边为12米,它所对应的高应为15米。
易错分析>>
忽略平行四边形中底与高的对应
因为直线外一点到这条直线的垂直线段最短,所以比高短的那条边是这条高对应的底。计算平行四边形的面积时,要正确选择数据,一定要用底乘所对应的高,可画图推理。
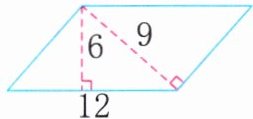
5. (生活应用)如图(单位:米),张伯伯有一块平行四边形菜地,这块菜地的面积是多少平方米?如果在这块菜地四周围上篱笆,那么至少要多少米篱笆?

答案:
12×6=72(平方米) 72÷9=8(米) (8+12)×2=40(米) 解析:先用一组对应的底和高求出平行四边形菜地的面积,再用平行四边形菜地的面积除以另一条高求出平行四边形菜地的另一条边,最后求出平行四边形菜地的周长,即至少要的篱笆的长。
6. 一个平行四边形,如果底不变,高增加8厘米,那么面积会增加320平方厘米;如果高不变,底减少6厘米,那么面积会减少90平方厘米。这个平行四边形的面积是多少平方厘米?
答案:
320÷8=40(厘米) 90÷6=15(厘米) 40×15=600(平方厘米) 解析:根据题意可知,底不变,高增加8厘米,高增加后的平行四边形的底和这个平行四边形的底相同;高不变,底减少6厘米,底减少后的平行四边形的高和这个平行四边形的高相同。根据高或底的变化以及对应的面积的变化,分别求出这个平行四边形的底和高,再求面积即可。
查看更多完整答案,请扫码查看


