《2025年拔尖特训五年级数学上册苏教版》

1.(几何直观)如图,一个平行四边形相邻两边的长分别是12厘米和8厘米,高是10厘米,沿高剪拼成长方形,长方形的面积是(80)平方厘米,周长是(36)厘米。

答案： 80 36 解析:剪拼成的长方形的长是平行四边形的高,宽是平行四边形的高对应的底。

2. 如图,一个由细木条钉成的长方形框架,长8厘米,宽6厘米,它的面积是(48)平方厘米。若把它拉成一个高是5厘米的平行四边形,则平行四边形的周长是(28)厘米,面积是(40)平方厘米。

答案： 48 28 40 解析:拉成的平行四边形相邻的两条边是原长方形框架的长和宽,且平行四边形5厘米的高对应的底是8厘米。

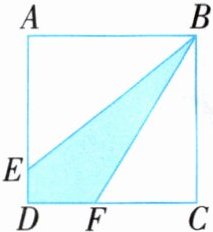
3. 如图,正方形的边长为10厘米,AE为8厘米,CF为6厘米,求涂色部分的面积。
]

答案： 10×10 - 8×10÷2 - 6×10÷2 = 30(平方厘米) 解析:涂色部分的面积 = 正方形ABCD的面积 - 三角形ABE的面积 - 三角形BCF的面积。

4. 如图,两个正方形的边长分别为6分米和4分米,求涂色部分的面积。
]

答案： 6×6 + 4×4 - 6×6÷2 - (6 + 4)×4÷2 = 14(平方分米) 解析:涂色部分的面积等于两个正方形的面积和减去两个空白三角形的面积。

5. 如图(单位:米),在一块长方形土地上,修建两条宽度一样的人行道,余下的部分铺成草坪。草坪的面积是多少平方米?
]

答案： 100×70 = 7000(平方米) 解析:通过平移,可将3块草坪合并成一个长100米、宽70米的长方形。

6.(社会生活)如图所示为王伯伯家的一块长方形地,长是18米,宽是10米,政府规划在中间修两条石子路(涂色部分)。如果当地每平方米的征地补贴是100元,那么王伯伯能领到多少元征地补贴?
]

答案：
[18×10 - (18 - 2)×(10 - 3)]×100 = 6800(元) 解析:如图,通过平移,可将四块地拼成一个长是(18 - 2)米、宽是(10 - 3)米的长方形,用原来这块长方形地的面积减去拼成的长方形的面积就是两条石子路的面积和。

7. 实验小学有一块草地的形状是直角梯形(如图),两条隔离带把草地分成了三个三角形,其中有两个是等腰直角三角形。已知直角梯形较短的一条腰长10米,求这块草地的面积。
]

答案： 10×10÷2 = 50(平方米) 解析:由题意可知,直角梯形的高是10米,且该梯形中左上角和左下角的两个三角形是等腰直角三角形,所以直角梯形上、下底的和等于直角梯形的高,即10米,用上、下底的和×高÷2即可求出这块草地的面积。