《2025年拔尖特训五年级数学上册苏教版》

1. 计算下面图形中涂色部分的面积。
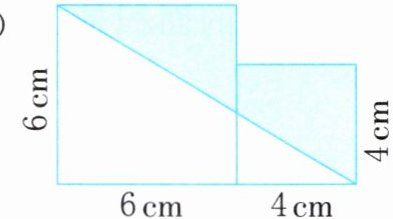
(1)
(2)

答案： 1.
(1)6×6+4×4−(6+4)×6÷2=22(cm²)
(2)8×8÷2+8×4÷2=48(dm²)

2.(地域特色)漳州八宝印泥是书法家酷爱的珍品。该印泥制作技艺传承人小孙在制作一份作品时想给下面的图案上色,则涂色部分的面积有多大？

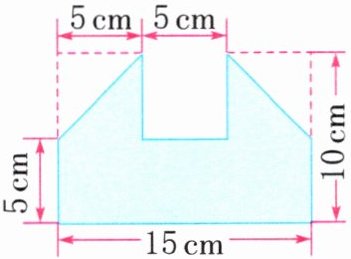
答案： 2.15×5+(15−5)×(10−5)÷2=100(cm²)

3. 实验小学要重新给教室的门内外两面刷油漆(空白部分是玻璃),如果每平方米需要花费38元,那么刷40扇这样的门一共需要花费多少元？

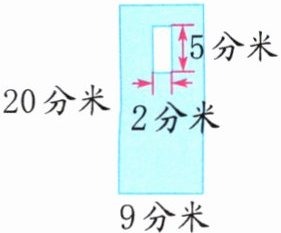
答案： 3.(9×20−2×5)×2=340(平方分米)　340×40=13600(平方分米)　13600平方分米=136平方米　136×38=5168(元)

4. 下面的涂色部分中,面积最大的是(C)。(每个小方格表示1平方厘米)
A.
B.
C.
D.

答案： 4.C

5.(推理意识)求涂色部分的面积。(单位：厘米)

答案： 5.30×40÷2×2÷50=24(厘米)　20×24÷2=240(平方厘米)　解析:先求出空白直角三角形的面积，从而可求出其斜边上的高，即梯形的高。再根据两个涂色三角形的底之和等于梯形的上底，两个涂色三角形的高相等，且等于梯形的高，即可求出涂色部分的面积。

6. 如图,将四张长20厘米、宽3厘米的长方形纸条互相垂直粘贴在一起,平放在地面上,地面被盖住的面积是多少？

答案： 6.20×3×4−3×3×4=204(平方厘米)　解析:粘贴在一起的四张纸条有四处重叠，每处重叠的部分都是边长为3厘米的小正方形。地面被盖住的面积即四张纸条的总面积减去重叠部分的四个小正方形的总面积。

7. 求下面四边形的面积。

答案：
7.14×14÷2−8×8÷2=66(cm²)　解析:可以把这个图形的两条边延长，变成一个直角三角形,如图,∠A=∠E=45°,所以三角形ABE是等腰直角三角形,AB=BE=14cm。在直角三角形CDE 中,由∠E=45°,可知三角形CDE是等腰直角三角形，所以CD=ED=8cm,所求四边形的面积就是三角形ABE的面积与三角形CDE的面积的差。