第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
10. 类比归纳思想 如图,在平面直角坐标系中,原点$O$第一次跳动到点$A_{1}(0,1)$,第二次从点$A_{1}$跳动到点$A_{2}(1,2)$,第三次从点$A_{2}$跳动到点$A_{3}(-1,3)$,第四次从点$A_{3}$跳动到点$A_{4}(-1,4)$……按此规律进行下去,点$A_{2025}$的坐标是(

A.$(674,2025)$
B.$(675,2025)$
C.$(-674,2025)$
D.$(-675,2025)$
D
)
A.$(674,2025)$
B.$(675,2025)$
C.$(-674,2025)$
D.$(-675,2025)$
答案:
D
11.(辽宁中考)在平面直角坐标系中,线段$AB$的端点坐标分别为$A(2,-1)$,$B(1,0)$,将线段$AB$平移后,点$A$的对应点$A'$的坐标为$(2,1)$,则点$B$的对应点$B'$的坐标为______
(1,2)
.
答案:
(1,2)
12. 若第一象限内的点$P(x,y)$满足$|x| = 4$,$y^{2} = 9$,则点$P$的坐标是______
(4,3)
。
答案:
(4,3)
13. 情境题 地理位置 (贵州中考)如图所示为贵阳市城市轨道交通运营的部分示意图.若以喷水池为原点,分别以正东、正北方向为$x$轴、$y$轴的正方向建立平面直角坐标系,贵阳北站的坐标是$(-2,7)$,则龙洞堡机场的坐标是______.
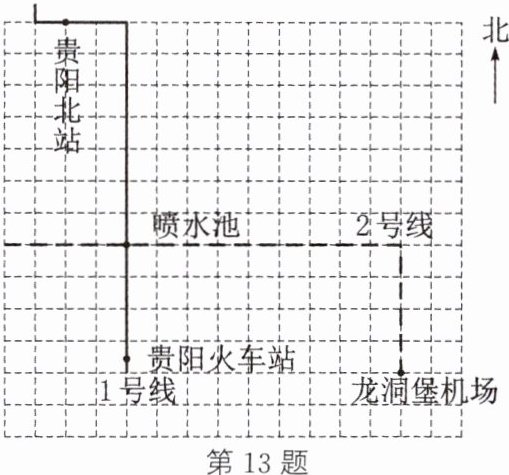
13. 情境题 地理位置 (贵州中考)如图所示为贵阳市城市轨道交通运营的部分示意图.若以喷水池为原点,分别以正东、正北方向为$x$轴、$y$轴的正方向建立平面直角坐标系,贵阳北站的坐标是$(-2,7)$,则龙洞堡机场的坐标是__


13. 情境题 地理位置 (贵州中考)如图所示为贵阳市城市轨道交通运营的部分示意图.若以喷水池为原点,分别以正东、正北方向为$x$轴、$y$轴的正方向建立平面直角坐标系,贵阳北站的坐标是$(-2,7)$,则龙洞堡机场的坐标是__
(9,−4)
__.
答案:
(9,−4)
14. 新考向 传统文化 (台州中考)在象棋棋盘(部分)中建立如图所示的平面直角坐标系.已知“车”所在位置的坐标为$(-2,2)$,则“炮”所在位置的坐标为______.
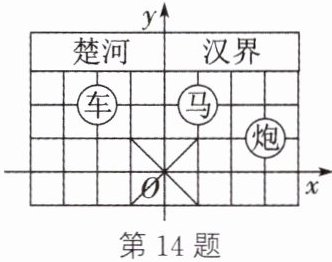
14. 新考向 传统文化 (台州中考)在象棋棋盘(部分)中建立如图所示的平面直角坐标系.已知“车”所在位置的坐标为$(-2,2)$,则“炮”所在位置的坐标为______.

14. 新考向 传统文化 (台州中考)在象棋棋盘(部分)中建立如图所示的平面直角坐标系.已知“车”所在位置的坐标为$(-2,2)$,则“炮”所在位置的坐标为__


14. 新考向 传统文化 (台州中考)在象棋棋盘(部分)中建立如图所示的平面直角坐标系.已知“车”所在位置的坐标为$(-2,2)$,则“炮”所在位置的坐标为______.

14. 新考向 传统文化 (台州中考)在象棋棋盘(部分)中建立如图所示的平面直角坐标系.已知“车”所在位置的坐标为$(-2,2)$,则“炮”所在位置的坐标为__
(3,1)
__.
答案:
(3,1)
15. 已知点$P(3a - 6,1 - a)$在$x$轴上,则点$P$的坐标为
(−3,0)
.
答案:
(−3,0)
易错提示
未正确理解坐标轴上点的坐标特征致错
点的坐标是指分别过这个点向x轴、y轴作垂线段,垂足在数轴上所对的数就是这个点的横、纵坐标。若点在x轴上,则点的纵坐标为0;若点在y轴上,则点的横坐标为0。不能很好地理解点的横、纵坐标的求法,就会错误地得出点的坐标。
易错提示
未正确理解坐标轴上点的坐标特征致错
点的坐标是指分别过这个点向x轴、y轴作垂线段,垂足在数轴上所对的数就是这个点的横、纵坐标。若点在x轴上,则点的纵坐标为0;若点在y轴上,则点的横坐标为0。不能很好地理解点的横、纵坐标的求法,就会错误地得出点的坐标。
16. 如果点$P(x,y)$的坐标满足$x + y = xy$,那么称$P$为“和谐点”。若“和谐点”$P$到$x$轴的距离为$2$,则点$P$的坐标为
(2,2)或($\frac{2}{3}$,−2)
。
答案:
(2,2)或($\frac{2}{3}$,−2) 解析:
∵点P的坐标为(x,y),“和谐点”P到x轴的距离为2,
∴|y|=2。
∴y=±2。将y=2代入x+y=xy,得x+2=2x,解得x=2。
∴点P 的坐标为(2,2)。将y=−2代入x+y=xy,得x−2=−2x,解得x=$\frac{2}{3}$。
∴点P的坐标为($\frac{2}{3}$,−2)。综上所述,点P的坐标为(2,2)或($\frac{2}{3}$,−2)。
∵点P的坐标为(x,y),“和谐点”P到x轴的距离为2,
∴|y|=2。
∴y=±2。将y=2代入x+y=xy,得x+2=2x,解得x=2。
∴点P 的坐标为(2,2)。将y=−2代入x+y=xy,得x−2=−2x,解得x=$\frac{2}{3}$。
∴点P的坐标为($\frac{2}{3}$,−2)。综上所述,点P的坐标为(2,2)或($\frac{2}{3}$,−2)。
17.(10分)情境题 地理位置 如图所示为小明家和学校所在地的简单地图,且$OA= 2cm$,$OB= 2.5cm$,$OP= 4cm$,$C为OP$的中点.
(1)图中与小明家距离相同的是哪些地方?
∵C为OP的中点,∴OC=$\frac{1}{2}$OP=$\frac{1}{2}$×4=2(cm)。∵OA=2cm,∴与小明家距离相同的是
(2)学校、商场、公园、停车场分别在小明家的什么方向上?哪两个地方的方向相同?
学校:
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多少米?
由题意,得图上1cm表示实际400÷2=200(m),∴商场距离小明家

(1)图中与小明家距离相同的是哪些地方?
∵C为OP的中点,∴OC=$\frac{1}{2}$OP=$\frac{1}{2}$×4=2(cm)。∵OA=2cm,∴与小明家距离相同的是
学校和公园
。(2)学校、商场、公园、停车场分别在小明家的什么方向上?哪两个地方的方向相同?
学校:
北偏东45°
,商场:北偏西30°
,公园:南偏东60°
,停车场:南偏东60°
。公园和停车场
的方向相同。(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多少米?
由题意,得图上1cm表示实际400÷2=200(m),∴商场距离小明家
2.5×200 = 500(m)
,停车场距离小明家4×200 = 800(m)
。
答案:
(1)
∵C为OP的中点,
∴OC=$\frac{1}{2}$OP=$\frac{1}{2}$×4=2(cm)。
∵OA=2cm,
∴与小明家距离相同的是学校和公园。
(2)学校:北偏东45°,商场:北偏西30°,公园:南偏东60°,停车场:南偏东60°。公园和停车场的方向相同。
(3)由题意,得图上1cm表示实际400÷2=200(m),
∴商场距离小明家2.5×200=500(m),停车场距离小明家4×200=800(m)。
(1)
∵C为OP的中点,
∴OC=$\frac{1}{2}$OP=$\frac{1}{2}$×4=2(cm)。
∵OA=2cm,
∴与小明家距离相同的是学校和公园。
(2)学校:北偏东45°,商场:北偏西30°,公园:南偏东60°,停车场:南偏东60°。公园和停车场的方向相同。
(3)由题意,得图上1cm表示实际400÷2=200(m),
∴商场距离小明家2.5×200=500(m),停车场距离小明家4×200=800(m)。
查看更多完整答案,请扫码查看


