《2025年通城学典暑期升级训练七年级数学》

22. (8 分)新情境 日常生活 (安徽中考)根据经营情况,公司对某商品在甲、乙两地的销售单价进行了如下调整：甲地上涨$10\%$,乙地降价 5 元.已知调整前甲地的销售单价比乙地的销售单价少 10 元,调整后甲地的销售单价比乙地的销售单价少 1 元,求调整前甲、乙两地该商品的销售单价.

答案： 设调整前甲、乙两地该商品的销售单价分别为 $ x $ 元、$ y $ 元。根据题意，得 $ \begin{cases} x + 10 = y, \\ (1 + 10\%)x + 1 = y - 5, \end{cases} $ 解得 $ \begin{cases} x = 40, \\ y = 50. \end{cases} $
∴ 调整前甲、乙两地该商品的销售单价分别为 40 元、50 元。

23. (10 分)直线$MN$与直线$PQ$垂直相交于点$O$，点$A$在射线$OP$上运动，点$B$在射线$OM$上运动。
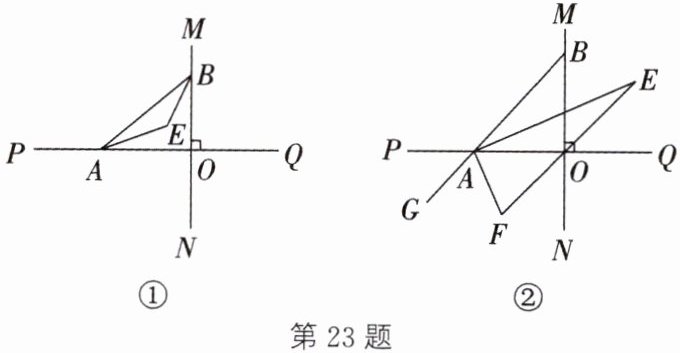
(1)如图①，$AE$，$BE$分别是$∠BAO$和$∠ABO$的平分线。在点$A$，$B$的运动过程中，$∠AEB$的度数是否会发生变化？若发生变化，请说明理由；若不发生变化，请求出$∠AEB$的度数。
$ \angle AEB $的度数不发生变化。∵ 直线 $ MN $ 与直线 $ PQ $ 垂直相交于点 $ O $，∴ $ \angle AOB = 90^\circ $。∴ $ \angle OAB + \angle OBA = 90^\circ $。∵ $ AE $，$ BE $ 分别是 $ \angle BAO $ 和 $ \angle ABO $ 的平分线，∴ $ \angle BAE = \frac{1}{2} \angle OAB $，$ \angle ABE = \frac{1}{2} \angle ABO $。∴ $ \angle BAE + \angle ABE = \frac{1}{2} (\angle OAB + \angle ABO) = \frac{1}{2} × 90^\circ = 45^\circ $。∴ $ \angle AEB = 180^\circ - 45^\circ = 135^\circ $。
(2)如图②，延长$BA$至点$G$，$∠BAO$，$∠OAG$的平分线与$∠BOQ$的平分线所在的直线分别相交于点$E$，$F$，求$∠EAF$的度数。在三角形$AEF$中，如果有一个角的度数是另一个角的 3 倍，求$∠ABO$的度数。
∵ $ AE $，$ AF $ 分别是 $ \angle BAO $ 和 $ \angle OAG $ 的平分线，∴ $ \angle EAO = \frac{1}{2} \angle BAO $，$ \angle FAO = \frac{1}{2} \angle GAO $。∴ $ \angle EAF = \angle EAO + \angle FAO = \frac{1}{2} (\angle BAO + \angle GAO) = \frac{1}{2} × 180^\circ = 90^\circ $。∵ $ OE $ 平分 $ \angle BOQ $，∴ $ \angle EOQ = \frac{1}{2} \angle BOQ $。∴ 易得 $ \angle E = \angle EOQ - \angle EAO = \frac{1}{2} (\angle BOQ - \angle BAO) = \frac{1}{2} \angle ABO $，即 $ \angle ABO = 2 \angle E $。在三角形 $ AEF $ 中，∵ 有一个角的度数是另一个角的 3 倍，易得 $ \angle E $，$ \angle F $ 不可能等于 $ 3 \angle EAF $，∴ 分四种情况讨论。① 当 $ \angle EAF = 3 \angle E $ 时，∵ $ \angle EAF = 90^\circ $，∴ $ \angle E = 30^\circ $。∴ $ \angle ABO = 60^\circ $。② 当 $ \angle EAF = 3 \angle F $ 时，∵ $ \angle EAF = 90^\circ $，∴ $ \angle F = 30^\circ $。∴ $ \angle E = 60^\circ $。∴ $ \angle ABO = 120^\circ $（不合题意，舍去）。③ 当 $ \angle F = 3 \angle E $ 时，∵ $ \angle EAF = 90^\circ $，∴ $ \angle F + \angle E = 90^\circ $。∴ $ \angle E = 22.5^\circ $。∴ $ \angle ABO = 45^\circ $。④ 当 $ \angle E = 3 \angle F $ 时，∵ $ \angle EAF = 90^\circ $，∴ $ \angle F + \angle E = 90^\circ $。∴ $ \angle E = 67.5^\circ $。∴ $ \angle ABO = 135^\circ $（不合题意，舍去）。综上所述，$ \angle ABO $ 的度数为 $ 60^\circ $ 或 $ 45^\circ $。

答案：
(1) $ \angle AEB $ 的度数不发生变化。
∵ 直线 $ MN $ 与直线 $ PQ $ 垂直相交于点 $ O $，
∴ $ \angle AOB = 90^\circ $。
∴ $ \angle OAB + \angle OBA = 90^\circ $。
∵ $ AE $，$ BE $ 分别是 $ \angle BAO $ 和 $ \angle ABO $ 的平分线，
∴ $ \angle BAE = \frac{1}{2} \angle OAB $，$ \angle ABE = \frac{1}{2} \angle ABO $。
∴ $ \angle BAE + \angle ABE = \frac{1}{2} (\angle OAB + \angle ABO) = \frac{1}{2} × 90^\circ = 45^\circ $。
∴ $ \angle AEB = 180^\circ - 45^\circ = 135^\circ $。
(2)
∵ $ AE $，$ AF $ 分别是 $ \angle BAO $ 和 $ \angle OAG $ 的平分线，
∴ $ \angle EAO = \frac{1}{2} \angle BAO $，$ \angle FAO = \frac{1}{2} \angle GAO $。
∴ $ \angle EAF = \angle EAO + \angle FAO = \frac{1}{2} (\angle BAO + \angle GAO) = \frac{1}{2} × 180^\circ = 90^\circ $。
∵ $ OE $ 平分 $ \angle BOQ $，
∴ $ \angle EOQ = \frac{1}{2} \angle BOQ $。
∴ 易得 $ \angle E = \angle EOQ - \angle EAO = \frac{1}{2} (\angle BOQ - \angle BAO) = \frac{1}{2} \angle ABO $，即 $ \angle ABO = 2 \angle E $。在三角形 $ AEF $ 中，
∵ 有一个角的度数是另一个角的 3 倍，易得 $ \angle E $，$ \angle F $ 不可能等于 $ 3 \angle EAF $，
∴ 分四种情况讨论。① 当 $ \angle EAF = 3 \angle E $ 时，
∵ $ \angle EAF = 90^\circ $，
∴ $ \angle E = 30^\circ $。
∴ $ \angle ABO = 60^\circ $。② 当 $ \angle EAF = 3 \angle F $ 时，
∵ $ \angle EAF = 90^\circ $，
∴ $ \angle F = 30^\circ $。
∴ $ \angle E = 60^\circ $。
∴ $ \angle ABO = 120^\circ $（不合题意，舍去）。③ 当 $ \angle F = 3 \angle E $ 时，
∵ $ \angle EAF = 90^\circ $，
∴ $ \angle F + \angle E = 90^\circ $。
∴ $ \angle E = 22.5^\circ $。
∴ $ \angle ABO = 45^\circ $。④ 当 $ \angle E = 3 \angle F $ 时，
∵ $ \angle EAF = 90^\circ $，
∴ $ \angle F + \angle E = 90^\circ $。
∴ $ \angle E = 67.5^\circ $。
∴ $ \angle ABO = 135^\circ $（不合题意，舍去）。综上所述，$ \angle ABO $ 的度数为 $ 60^\circ $ 或 $ 45^\circ $。