《2025年通城学典暑期升级训练七年级数学》

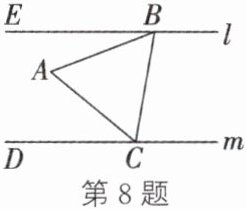
8. (泰安中考)如图,直线$l// m$,等边三角形ABC的两个顶点B,C分别落在直线l,m上.若$∠ABE= 21^{\circ }$,则$∠ACD$的度数为 (B)



A.$45^{\circ }$
B.$39^{\circ }$
C.$29^{\circ }$
D.$21^{\circ }$

答案： B

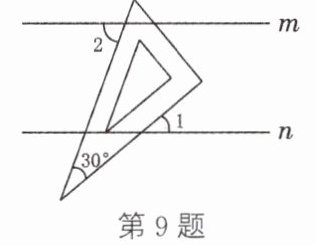
9. (巴中中考)如图,直线$m// n$,一块含有$30^{\circ }$角的三角尺按如图所示的方式放置.若$∠1= 40^{\circ }$,则$∠2$的度数为 (A)


A.$70^{\circ }$
B.$60^{\circ }$
C.$50^{\circ }$
D.$40^{\circ }$

答案： A

10. (潍坊中考)一种路灯的示意图如图所示,其底部支架AB与吊线FG平行,灯杆CD与底部支架AB所成锐角$∠α=15^{\circ }$.顶部支架EF与灯杆CD所成锐角$∠β=45^{\circ }$,则EF与FG所成锐角的度数为 ( )


A.$60^{\circ }$
B.$55^{\circ }$
C.$50^{\circ }$
D.$45^{\circ }$

答案：
A 解析: 如图, 过点 $E$ 作 $EH// AB.\because AB// FG,\therefore AB// EH// FG.\therefore \angle BEH=\angle \alpha=15^{\circ},\angle FEH+\angle EFG=180^{\circ}.\because \angle \beta=45^{\circ},\therefore \angle FEH=180^{\circ}-45^{\circ}-15^{\circ}=120^{\circ}.\therefore \angle EFG=180^{\circ}-\angle FEH=180^{\circ}-120^{\circ}=60^{\circ}.\therefore EF$ 与 $FG$ 所成锐角的度数为 $60^{\circ}$.

11. 新考法 过程性学习 两条平行线间的拐点问题经常可以通过作一条直线的平行线来解决.
例如：如图①,$MN// PQ$,点C,B分别在直线MN,PQ上,点A在直线MN,PQ之间,求证：$∠CAB= ∠MCA+∠PBA$.
证明：如图①,过点A作$AD// MN$.
$\because MN// PQ,AD// MN$,
$\therefore AD// MN// PQ$.
$\therefore ∠MCA= ∠DAC,∠PBA= ∠DAB$.
$\therefore ∠CAB= ∠DAC+∠DAB= ∠MCA+∠PBA$.
已知直线$AB// CD$,P为平面内一点,连接PA,PD.
(1)如图②.若$∠A= 50^{\circ },∠D= 150^{\circ }$,求$∠APD$的度数.
(2)如图③,设$∠PAB= α,∠CDP= β$,则α,β,$∠P$之间的数量关系为____.
(3)如图④,$AP⊥PD$,AN与DP交于点O,DN平分$∠PDC$.若$∠PAN+\frac {1}{2}∠PAB= ∠P$,运用(2)中的结论,求$∠N$的度数.

答案：

(1) 如图, 过点 $P$ 作 $PE// AB.\because AB// CD,PE// AB,\therefore AB// PE// CD.\therefore \angle APE=\angle A=50^{\circ},\angle DPE+\angle D=180^{\circ}.\therefore \angle DPE=180^{\circ}-150^{\circ}=30^{\circ}.\therefore \angle APD=\angle APE+\angle DPE=50^{\circ}+30^{\circ}=80^{\circ}$.
(2) $\alpha+\beta-\angle P=180^{\circ}$.
(3) $\because AP\perp PD,\therefore \angle P=90^{\circ}.\because \angle PAN+\frac{1}{2}\angle PAB=\angle P,\therefore \angle PAN+\frac{1}{2}\angle PAB=90^{\circ}.\because \angle POA+\angle PAN=180^{\circ}-\angle P=90^{\circ},\therefore \angle POA=\frac{1}{2}\angle PAB.\because \angle POA=\angle NOD,\therefore \angle NOD=\frac{1}{2}\angle PAB.\because DN$ 平分 $\angle PDC,\therefore \angle ODN=\frac{1}{2}\angle PDC.\therefore \angle N=180^{\circ}-\angle NOD-\angle ODN=180^{\circ}-\frac{1}{2}(\angle PAB+\angle PDC)$. 由
(2), 得 $\angle PDC+\angle PAB-\angle P=180^{\circ},\therefore \angle PDC+\angle PAB=180^{\circ}+\angle P.\therefore \angle N=180^{\circ}-\frac{1}{2}(\angle PAB+\angle PDC)=180^{\circ}-\frac{1}{2}(180^{\circ}+\angle P)=180^{\circ}-\frac{1}{2}×(180^{\circ}+90^{\circ})=45^{\circ}$.