《2025年新暑假生活七年级数学华师大版》

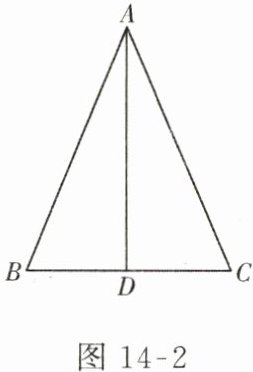
3. 如图 14 - 2,在$\triangle ABC$中,$AD⊥BC$于 D.请你再添加一个条件,就可以确定$\triangle ABC$是等腰三角形.你添加的条件是$BD = CD$（或$\angle BAD=\angle CAD$等，答案不唯一）.

答案： $BD = CD$（或$\angle BAD=\angle CAD$等，答案不唯一）

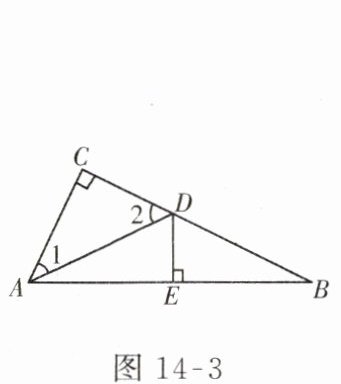
4. 如图 14 - 3,$∠C=90^{\circ }$,DE 垂直平分 AB,$∠1:∠2=2:3$,则$∠1$的度数为____.


4. 如图 14 - 3,$∠C=90^{\circ }$,DE 垂直平分 AB,$∠1:∠2=2:3$,则$∠1$的度数为$22.5^{\circ}$.

答案： $22.5^{\circ}$

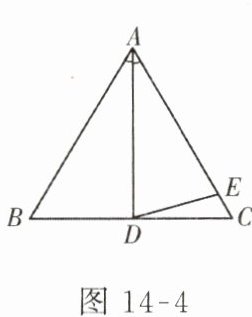
5. 如图 14 - 4,在$\triangle ABC$中,$AB=AC,∠BAD=∠DAC=30^{\circ }$,且$AD=AE$,则$∠AED=$$75^{\circ}$.

答案： $75^{\circ}$

三、解答题.
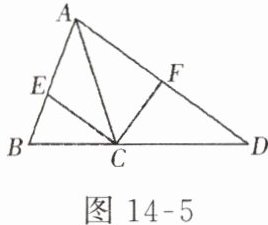
如图 14 - 5 所示,在$\triangle ABC$中,D 是 BC 延长线上的一点,且$CD=AC$,F 为AD 的中点,CE 平分$∠ACB$交 AB 于 E.求证:$CE⊥CF$.

证明：∵ $ AC = CD $，$ AF = DF $，
∴ 根据三线合一，$ \angle ACF = \frac{1}{2} \angle ACD $，
又 ∵ $ \angle ACE = \frac{1}{2} \angle ACB $，
∴ $ \angle ECF = \frac{1}{2} ( \angle ACB + \angle ACD ) = 90 ^ { \circ } $，∴ $ CE \perp CF $。

答案： 证明：
∵ $ AC = CD $，$ AF = DF $，
∴ 根据三线合一，$ \angle ACF = \frac{1}{2} \angle ACD $，
又
∵ $ \angle ACE = \frac{1}{2} \angle ACB $，
∴ $ \angle ECF = \frac{1}{2} ( \angle ACB + \angle ACD ) = 90 ^ { \circ } $，
∴ $ CE \perp CF $。