2025年新暑假生活七年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新暑假生活七年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2.过四边形一个顶点的对角线可以把四边形分成两个三角形;过五边形一个顶点的对角线可以把五边形分成______个三角形;过六边形一个顶点的对角线可以把六边形分成______个三角形.经过上面的探究,你可以归纳出过$n边形一个顶点的对角线可以把n$边形分成多少个三角形吗?(用含$n$的代数式表示)请画出一个五边形,以特殊代替一般来证明$n$边形内角和的度数.
答案:
三 四
画图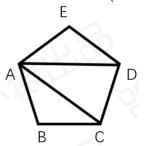
证明
∴n边形内角和为(n- 2)·180°
三 四
画图

证明
从n边形一个顶点引对角线可以把n边形分成(n-2)个三角形
已知五边形ABCDE,
连接AC、AD,把五边形分成(5-2),即3个三角形,3个三角形的内角和等于五边形的内角和,
为3×180°=540°
∴n边形内角和为(n- 2)·180°
1. 某市一所中学在教学楼前设计了一个小广场(图13 - 1),正方形广场地面的边长为$40$米,中心建了一个直径为$20$米的圆形花坛,四角各留一个边长为$10$米的小正方形花坛,种植花草,图中阴影部分计划铺设地砖,请问:
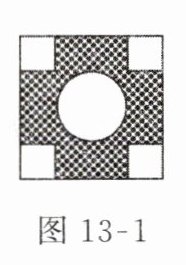
(1)该设计图是轴对称图形吗?若是,有几条对称轴?(
(2)若广场铺地砖,至少需购地砖多少平方米?(

(1)该设计图是轴对称图形吗?若是,有几条对称轴?(
是轴对称图形,有 4 条对称轴
)(2)若广场铺地砖,至少需购地砖多少平方米?(
886 平方米
)
答案:
(1)是轴对称图形,有 4 条对称轴 (2)886 平方米
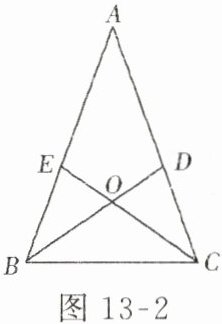
2. 如图13 - 2,在$\triangle ABC$中,$AB = AC$,$BD$、$CE$分别平分$\angle ABC$、$\angle ACB$,并且$BD$、$CE$相交于点$O$,请问$\triangle OBC$是什么三角形?并说明理由.
解:因为$AB = AC$,
所以$\angle ABC=\angle ACB$。
又因为$BD$、$CE$分别平分$\angle ABC$、$\angle ACB$,
所以$\angle OBC=\frac{1}{2}\angle ABC$,$\angle OCB=\frac{1}{2}\angle ACB$。
则$\angle OBC = \angle OCB$。
根据等角对等边,可得$OB = OC$。
所以$\triangle OBC$是
解:因为$AB = AC$,
所以$\angle ABC=\angle ACB$。
又因为$BD$、$CE$分别平分$\angle ABC$、$\angle ACB$,
所以$\angle OBC=\frac{1}{2}\angle ABC$,$\angle OCB=\frac{1}{2}\angle ACB$。
则$\angle OBC = \angle OCB$。
根据等角对等边,可得$OB = OC$。
所以$\triangle OBC$是
等腰三角形
。
答案:
解:因为$AB = AC$,
所以$\angle ABC=\angle ACB$。
又因为$BD$、$CE$分别平分$\angle ABC$、$\angle ACB$,
所以$\angle OBC=\frac{1}{2}\angle ABC$,$\angle OCB=\frac{1}{2}\angle ACB$。
则$\angle OBC = \angle OCB$。
根据等角对等边,可得$OB = OC$。
所以$\triangle OBC$是等腰三角形。
所以$\angle ABC=\angle ACB$。
又因为$BD$、$CE$分别平分$\angle ABC$、$\angle ACB$,
所以$\angle OBC=\frac{1}{2}\angle ABC$,$\angle OCB=\frac{1}{2}\angle ACB$。
则$\angle OBC = \angle OCB$。
根据等角对等边,可得$OB = OC$。
所以$\triangle OBC$是等腰三角形。
查看更多完整答案,请扫码查看


