《2025年一本五年级数学苏教版暑假计算加应用题》

1. 小明用磁力球和磁力棒拼搭长方体框架(1 条棱处用 1 根磁力棒),已经拼搭好的部分如图所示。
(1) 他还需要用(2)个磁力球、(3)根 7 cm 长的磁力棒、(2)根 4 cm 长的磁力棒、(2)根 3 cm 长的磁力棒才可以拼搭成长方体框架。
(2) 拼搭好后,所用的磁力棒的总长是(56)cm。

答案： 解析：本题考查长方体的特征以及棱长总和的计算。
（1）长方体有$8$个顶点，$12$条棱，棱包括$4$条长、$4$条宽、$4$条高。
从图中可知，已经有$6$个磁力球（顶点），还需要$8 - 6 = 2$个磁力球。
已经有$1$条$7cm$长的棱，还需要$4 - 1 = 3$根$7cm$长的磁力棒。
已经有$2$条$4cm$长的棱，还需要$4 - 2 = 2$根$4cm$长的磁力棒。
已经有$2$条$3cm$长的棱，还需要$4 - 2 = 2$根$3cm$长的磁力棒。
所以，他还需要用$2$个磁力球、$3$根$7cm$长的磁力棒、$2$根$4cm$长的磁力棒、$2$根$3cm$长的磁力棒才可以拼搭成长方体框架。
（2）求所用磁力棒的总长，就是求这个长方体的棱长总和。
长方体棱长总和$ = 4×$长$ + 4×$宽$ + 4×$高。
已知长方体的长是$7cm$、宽是$4cm$、高是$3cm$，则总长为：
$4×7 + 4×4 + 4×3$
$ = 28 + 16 + 12$
$ = 56$（$cm$）
答案：
(1) $2$；$3$；$2$；$2$
(2) $56$

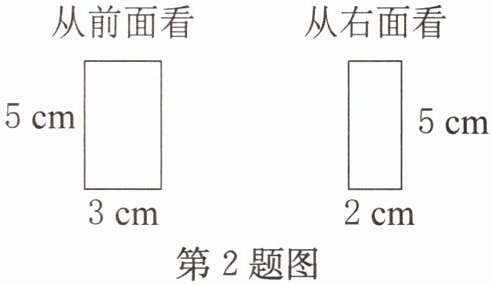
2. 一个长方体从前面和右面看到的图形如图所示,从上面看到的图形的面积是(6)cm²。

答案： 解析：本题考查长方体不同面的形状及面积计算。
从前面看到的图形是一个长为$5cm$、宽为$3cm$的长方形，从右面看到的图形是一个长为$5cm$、宽为$2cm$的长方形。
由此可推出长方体的长、宽、高分别为$3cm$、$2cm$、$5cm$。
从上面看到的图形是一个长为$3cm$、宽为$2cm$的长方形。
根据长方形面积公式$S = a× b$（其中$S$为长方形面积，$a$为长方形的长，$b$为长方形的宽），可得从上面看到的图形的面积为$3×2 = 6(cm^2)$。
答案：$6$。

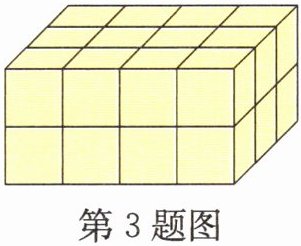
3. 如图,一个长方体是由棱长 1 cm 的小正方体搭成的,这个长方体的长是(6)cm,宽是(3)cm,高是(2)cm,棱长和是(44)cm。

答案： 解析：从图中可以看出，这个长方体沿着长有$6$个小正方体，沿着宽有$3$个小正方体，沿着高有$2$个小正方体。
因为小正方体的棱长是$1cm$，所以长方体的长就是$6$个小正方体棱长的长度，即$6×1 = 6cm$；
宽是$3$个小正方体棱长的长度，即$3×1 = 3cm$；
高是$2$个小正方体棱长的长度，即$2×1 = 2cm$。
长方体的棱长和$=$（长$+$宽$+$高）$×4$，把长$ = 6cm$，宽$ = 3cm$，高$ = 2cm$代入公式可得：
$(6 + 3 + 2)×4$
$=(9 + 2)×4$
$= 11×4$
$ = 44cm$。
答案：$6$；$3$；$2$；$44$。

4. 小本家有一顶长方体形状的蚊帐(如图),长方体的棱是用来固定蚊帐的钢管(地面四周没有),固定这样一顶蚊帐至少需要多少米长的钢管?

答案： 4.2×2+1.5×2+1.8×4=14.2(m)
答:固定这样一顶蚊帐至少需要14.2 m长的钢管。