2025年世超金典暑假乐园暑假七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世超金典暑假乐园暑假七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
四、看图填空
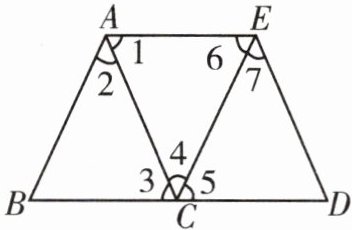
如图所示.
$\because ∠1= ∠3$(已知),$\therefore$
$\because ∠5= ∠B$(已知),$\therefore$
$\because ∠4= ∠7$(已知),$\therefore AC//$
$\therefore ∠1+∠AED= $
如图所示.
$\because ∠1= ∠3$(已知),$\therefore$
AE
$//$BD
(内错角相等,两直线平行
).$\because ∠5= ∠B$(已知),$\therefore$
AB
$//$CE
(同位角相等,两直线平行
).$\because ∠4= ∠7$(已知),$\therefore AC//$
DE
(内错角相等,两直线平行
).$\therefore ∠1+∠AED= $
$180^{\circ}$
(两直线平行,同旁内角互补
).
答案:
AE BD 内错角相等,两直线平行
AB CE 同位角相等,两直线平行
DE 内错角相等,两直线平行
$180^{\circ}$ 两直线平行,同旁内角互补
AB CE 同位角相等,两直线平行
DE 内错角相等,两直线平行
$180^{\circ}$ 两直线平行,同旁内角互补
1. 如图,$AB// CD$,直线$EF与AB$,$CD分别交于M$,$N$两点,过点$M作MG⊥EF交CD于G$点,过点$G作GH平分∠MGD$,$∠EMB= 40^{\circ }$.求$∠MGH$的度数.
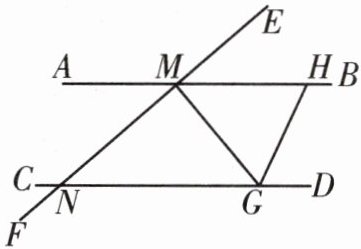
解:$\because MG\perp EF,\therefore \angle GME = 90^{\circ}$.
$\therefore \angle BMG = 90^{\circ}-\angle EMB = 90^{\circ}-40^{\circ}=$
$\because AB// CD,\therefore \angle BMG=\angle MGN =$
$\therefore \angle MGD =$
$\because GH$平分$\angle MGD$,
$\therefore \angle MGH=\frac{1}{2}\angle MGD =$

解:$\because MG\perp EF,\therefore \angle GME = 90^{\circ}$.
$\therefore \angle BMG = 90^{\circ}-\angle EMB = 90^{\circ}-40^{\circ}=$
50°
.$\because AB// CD,\therefore \angle BMG=\angle MGN =$
50°
.$\therefore \angle MGD =$
130°
.$\because GH$平分$\angle MGD$,
$\therefore \angle MGH=\frac{1}{2}\angle MGD =$
65°
.
答案:
解:$\because MG\perp EF,\therefore \angle GME = 90^{\circ}$.
$\therefore \angle BMG = 90^{\circ}-\angle EMB = 90^{\circ}-40^{\circ}=50^{\circ}$.
$\because AB// CD,\therefore \angle BMG=\angle MGN = 50^{\circ}$.
$\therefore \angle MGD = 130^{\circ}$.
$\because GH$平分$\angle MGD$,
$\therefore \angle MGH=\frac{1}{2}\angle MGD = 65^{\circ}$.
$\therefore \angle BMG = 90^{\circ}-\angle EMB = 90^{\circ}-40^{\circ}=50^{\circ}$.
$\because AB// CD,\therefore \angle BMG=\angle MGN = 50^{\circ}$.
$\therefore \angle MGD = 130^{\circ}$.
$\because GH$平分$\angle MGD$,
$\therefore \angle MGH=\frac{1}{2}\angle MGD = 65^{\circ}$.
2. 如图,$∠DAB+∠D= 180^{\circ }$,$AC平分∠DAB$,且$∠DAC= 30^{\circ }$.求$∠C$的度数.
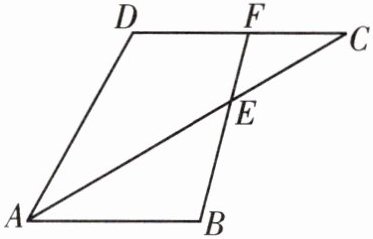
解:$\because AC$平分$\angle DAB,\angle DAC = 30^{\circ}$,
$\therefore \angle DAC=\angle BAC = 30^{\circ}$.
$\because \angle DAB+\angle D = 180^{\circ}$,
$\therefore AB// DC$.
$\therefore \angle C=\angle BAC =$

解:$\because AC$平分$\angle DAB,\angle DAC = 30^{\circ}$,
$\therefore \angle DAC=\angle BAC = 30^{\circ}$.
$\because \angle DAB+\angle D = 180^{\circ}$,
$\therefore AB// DC$.
$\therefore \angle C=\angle BAC =$
30°
.
答案:
解:$\because AC$平分$\angle DAB,\angle DAC = 30^{\circ}$,
$\therefore \angle DAC=\angle BAC = 30^{\circ}$.
$\because \angle DAB+\angle D = 180^{\circ}$,
$\therefore AB// DC$.
$\therefore \angle C=\angle BAC = 30^{\circ}$.
$\therefore \angle DAC=\angle BAC = 30^{\circ}$.
$\because \angle DAB+\angle D = 180^{\circ}$,
$\therefore AB// DC$.
$\therefore \angle C=\angle BAC = 30^{\circ}$.
3. 如图,$OP平分∠MON$,$PA// ON$,$PB// OM$.求证:(1)$∠2= ∠3$;(2)$PO平分∠APB$.
证明:(1)
(2)
证明:(1)
$\because PB// OM,\therefore \angle 1=\angle 3$.$\because OP$平分$\angle MON,\therefore \angle 1=\angle 2$.$\therefore \angle 2=\angle 3$.
(2)
$\because PA// ON,\therefore \angle 2=\angle APO$.又$\angle 3=\angle 2,\therefore \angle 3=\angle APO$.$\therefore PO$平分$\angle APB$.
答案:
证明:
(1)$\because PB// OM,\therefore \angle 1=\angle 3$.
$\because OP$平分$\angle MON,\therefore \angle 1=\angle 2$.
$\therefore \angle 2=\angle 3$.
(2)$\because PA// ON,\therefore \angle 2=\angle APO$.
又$\angle 3=\angle 2,\therefore \angle 3=\angle APO$.
$\therefore PO$平分$\angle APB$.
(1)$\because PB// OM,\therefore \angle 1=\angle 3$.
$\because OP$平分$\angle MON,\therefore \angle 1=\angle 2$.
$\therefore \angle 2=\angle 3$.
(2)$\because PA// ON,\therefore \angle 2=\angle APO$.
又$\angle 3=\angle 2,\therefore \angle 3=\angle APO$.
$\therefore PO$平分$\angle APB$.
六、趣味题
找规律,填空.

(
找规律,填空.

(
4
)规律是四周的数总和乘 2 等于中间的数.
答案:
4 规律是四周的数总和乘 2 等于中间的数.
查看更多完整答案,请扫码查看


