2025年世超金典暑假乐园暑假七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世超金典暑假乐园暑假七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,$AB// CD,∠1= ∠2$. 求证:$AM// CN$.

证明:

证明:
∵ AB // CD,∴ ∠EAB = ∠ECD。∵ ∠1 = ∠2,∴ ∠EAB - ∠1 = ∠ECD - ∠2。∴ ∠EAM = ∠ECN。∴ AM // CN
答案:
1. 证明:$\because AB // CD$,$\therefore \angle EAB = \angle ECD$。
$\because \angle 1 = \angle 2$,
$\therefore \angle EAB - \angle 1 = \angle ECD - \angle 2$。
$\therefore \angle EAM = \angle ECN$。$\therefore AM // CN$。
$\because \angle 1 = \angle 2$,
$\therefore \angle EAB - \angle 1 = \angle ECD - \angle 2$。
$\therefore \angle EAM = \angle ECN$。$\therefore AM // CN$。
2. 如图,直线$AB// CD,BC平分∠ABD,∠1= 65^{\circ }$. 求$∠2$的度数.
解:$\because$ 直线 $ AB // CD $,$\angle 1 = 65^{\circ}$,
$\therefore \angle 1 = \angle CBA = 65^{\circ}$。
$\because BC$ 平分 $\angle ABD$,
$\therefore \angle CBA = \angle CBD = 65^{\circ}$。
$\therefore \angle 2 = \angle 3 = 180^{\circ} - 65^{\circ} - 65^{\circ} =
解:$\because$ 直线 $ AB // CD $,$\angle 1 = 65^{\circ}$,
$\therefore \angle 1 = \angle CBA = 65^{\circ}$。
$\because BC$ 平分 $\angle ABD$,
$\therefore \angle CBA = \angle CBD = 65^{\circ}$。
$\therefore \angle 2 = \angle 3 = 180^{\circ} - 65^{\circ} - 65^{\circ} =
50^{\circ}
$。
答案:
2. 解:$\because$ 直线 $ AB // CD $,$\angle 1 = 65^{\circ}$,
$\therefore \angle 1 = \angle CBA = 65^{\circ}$。
$\because BC$ 平分 $\angle ABD$,
$\therefore \angle CBA = \angle CBD = 65^{\circ}$。
$\therefore \angle 2 = \angle 3 = 180^{\circ} - 65^{\circ} - 65^{\circ} = 50^{\circ}$。
$\therefore \angle 1 = \angle CBA = 65^{\circ}$。
$\because BC$ 平分 $\angle ABD$,
$\therefore \angle CBA = \angle CBD = 65^{\circ}$。
$\therefore \angle 2 = \angle 3 = 180^{\circ} - 65^{\circ} - 65^{\circ} = 50^{\circ}$。
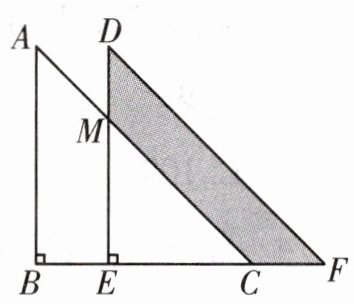
3. 如图,将直角三角形$ABC沿BC方向平移到直角三角形DEF$的位置,$AB= 6,BC= 6,BE= 2,DM= 2$. 求阴影部分$DMCF$的面积.
解:
因为$\triangle ABC$平移得到$\triangle DEF$,所以$\triangle ABC\cong\triangle DEF$。
那么$S_{\triangle ABC}=S_{\triangle DEF}$。
$S_{阴影DMCF}=S_{\triangle DEF}-S_{\triangle MEC}$,$S_{梯形ABEM}=S_{\triangle ABC}-S_{\triangle MEC}$。
所以$S_{阴影DMCF}=S_{梯形ABEM}$。
已知$AB = 6$,$BE = 2$,$ME=DE - DM$,又因为$DE = AB = 6$,$DM = 2$,所以$ME=6 - 2=4$。
根据梯形面积公式$S=\frac{(a + b)h}{2}$(其中$a$、$b$为梯形的上底和下底,$h$为梯形的高),这里$a = ME = 4$,$b = AB = 6$,$h = BE = 2$。
则$S_{梯形ABEM}=\frac{(4 + 6)×2}{2}$
$=\frac{10×2}{2}$
$= 10$。
所以阴影部分$DMCF$的面积为

解:
因为$\triangle ABC$平移得到$\triangle DEF$,所以$\triangle ABC\cong\triangle DEF$。
那么$S_{\triangle ABC}=S_{\triangle DEF}$。
$S_{阴影DMCF}=S_{\triangle DEF}-S_{\triangle MEC}$,$S_{梯形ABEM}=S_{\triangle ABC}-S_{\triangle MEC}$。
所以$S_{阴影DMCF}=S_{梯形ABEM}$。
已知$AB = 6$,$BE = 2$,$ME=DE - DM$,又因为$DE = AB = 6$,$DM = 2$,所以$ME=6 - 2=4$。
根据梯形面积公式$S=\frac{(a + b)h}{2}$(其中$a$、$b$为梯形的上底和下底,$h$为梯形的高),这里$a = ME = 4$,$b = AB = 6$,$h = BE = 2$。
则$S_{梯形ABEM}=\frac{(4 + 6)×2}{2}$
$=\frac{10×2}{2}$
$= 10$。
所以阴影部分$DMCF$的面积为
10
。
答案:
解:
因为$\triangle ABC$平移得到$\triangle DEF$,所以$\triangle ABC\cong\triangle DEF$。
那么$S_{\triangle ABC}=S_{\triangle DEF}$。
$S_{阴影DMCF}=S_{\triangle DEF}-S_{\triangle MEC}$,$S_{梯形ABEM}=S_{\triangle ABC}-S_{\triangle MEC}$。
所以$S_{阴影DMCF}=S_{梯形ABEM}$。
已知$AB = 6$,$BE = 2$,$ME=DE - DM$,又因为$DE = AB = 6$,$DM = 2$,所以$ME=6 - 2=4$。
根据梯形面积公式$S=\frac{(a + b)h}{2}$(其中$a$、$b$为梯形的上底和下底,$h$为梯形的高),这里$a = ME = 4$,$b = AB = 6$,$h = BE = 2$。
则$S_{梯形ABEM}=\frac{(4 + 6)×2}{2}$
$=\frac{10×2}{2}$
$= 10$。
所以阴影部分$DMCF$的面积为$10$。
因为$\triangle ABC$平移得到$\triangle DEF$,所以$\triangle ABC\cong\triangle DEF$。
那么$S_{\triangle ABC}=S_{\triangle DEF}$。
$S_{阴影DMCF}=S_{\triangle DEF}-S_{\triangle MEC}$,$S_{梯形ABEM}=S_{\triangle ABC}-S_{\triangle MEC}$。
所以$S_{阴影DMCF}=S_{梯形ABEM}$。
已知$AB = 6$,$BE = 2$,$ME=DE - DM$,又因为$DE = AB = 6$,$DM = 2$,所以$ME=6 - 2=4$。
根据梯形面积公式$S=\frac{(a + b)h}{2}$(其中$a$、$b$为梯形的上底和下底,$h$为梯形的高),这里$a = ME = 4$,$b = AB = 6$,$h = BE = 2$。
则$S_{梯形ABEM}=\frac{(4 + 6)×2}{2}$
$=\frac{10×2}{2}$
$= 10$。
所以阴影部分$DMCF$的面积为$10$。
四、趣味题
2,5,14,41,按照这个排列顺序,下一个数字应该是多少?
2,5,14,41,按照这个排列顺序,下一个数字应该是多少?
答案:
四、解:$ 5 - 2 = 3 = 3^{1} $,$ 14 - 5 = 9 = 3^{2} $,$ 41 - 14 = 27 = 3^{3} $,由此可知第 5 个数与 41 的差应该是 $ 3^{4} = 81 $,所以下一个数字是 $ 41 + 81 = 122 $。
查看更多完整答案,请扫码查看


