《2025年世超金典暑假乐园暑假七年级数学人教版》

2. $3-\sqrt {6}$的相反数是$\sqrt {6}-3$;$-\sqrt {2}$的倒数是$-\frac {1}{\sqrt {2}}$;绝对值等于$\sqrt {2}$的数是$\pm \sqrt {2}$.

答案： $\sqrt {6}-3$;$-\sqrt {2}$;$\pm \sqrt {2}$

3. 设$A= \sqrt {6}+\sqrt {2},B= \sqrt {5}+\sqrt {3}$,则$A,B$中数值较小的是A.(填“A”或“B”)

答案： A

4. 已知$a,b$互为相反数,$c,d$互为倒数,$m$的倒数等于它本身,则$\frac {cd}{m}+(a+b)m-|m|$等于0或-2.

答案： 0或-2

1. 将下列各数填入相应的集合中:
$6,-7\frac {1}{3},0,-100,+3.\dot {3},0.010010001…$(相邻的两个1之间依次多一个0),$+67,-\frac {π}{2},2000,-18$.
正整数集合:…$\{ 6,+67,2000,\}$;
负分数集合:…$\{ -7\frac {1}{3},\}$;
非负整数集合:…$\{ 6,0,+67,2000,\}$;
正有理数集合:…$\{ 6,+3.\dot {3},+67,2000,\}$;
无理数集合:…$\{ 0.010010001…$（相邻的两个1之间依次多一个0），$-\frac {π}{2},\}$.

答案： 正整数集合：$\{ 6,+67,2000,…\}$；负分数集合：$\{ -7\frac {1}{3},…\}$；非负整数集合：$\{ 6,0,+67,2000,…\}$；正有理数集合：$\{ 6,+3.\dot {3},+67,2000,…\}$；无理数集合：$\{ 0.010010001…$（相邻的两个1之间依次多一个0），$-\frac {π}{2},…\}$。

2. 在下列各数中,哪些是有理数,哪些是无理数?
$\sqrt {6},\frac {π}{2},1.23,\frac {22}{7},1.232232223…$(相邻的两个3之间依次多一个2),$-\sqrt {36},1.212112$.
有理数有:$1.23,\frac {22}{7},-\sqrt {36},1.212112$.
无理数有:$\sqrt {6},\frac {π}{2},1.232232223…$（相邻的两个3之间依次多一个2）.

答案： 有理数有：$1.23,\frac {22}{7},-\sqrt {36},1.212112$；无理数有：$\sqrt {6},\frac {π}{2},1.232232223…$（相邻的两个3之间依次多一个2）

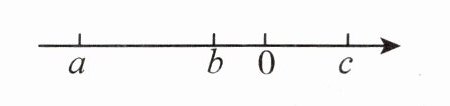
3. 已知实数$a,b,c$在数轴上的对应点如图所示,化简:$|a|-|a-b|+|c-a|+|b-c|$$=2c-2b-a$.

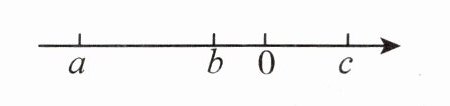
答案： 解：由数轴可知$a\lt b\lt0\lt c$。
1. 分析绝对值内式子的正负：
因为$a\lt0$，所以$\vert a\vert=-a$；
因为$a - b\lt0$，所以$\vert a - b\vert=-(a - b)=b - a$；
因为$c - a\gt0$，所以$\vert c - a\vert=c - a$；
因为$b - c\lt0$，所以$\vert b - c\vert=-(b - c)=c - b$。
2. 代入原式化简：
$\begin{aligned}\vert a\vert-\vert a - b\vert+\vert c - a\vert+\vert b - c\vert&=-a-(b - a)+(c - a)+(c - b)\\&=-a - b + a + c - a + c - b\\&=( - a + a - a)+(-b - b)+(c + c)\\&=-a-2b + 2c\end{aligned}$
所以$\vert a\vert-\vert a - b\vert+\vert c - a\vert+\vert b - c\vert=2c-2b - a$。

4. 若$a,b,c满足|a-3|+\sqrt {(5+b)^{2}}+\sqrt {c-1}= 0$,求式子$\frac {b-c}{a}$的值.-2.

答案： -2

四、趣味题
5,4,3,2,1.(猜一数学名词)倒数

答案： 倒数