2025年世超金典暑假乐园暑假七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世超金典暑假乐园暑假七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. 如下左图,$AC⊥BC$,$CD⊥AB$,则点$C到直线AB$的距离是线段 (
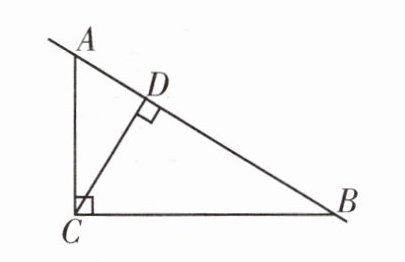
A.$CA$的长
B.$CD$的长
C.$CB$的长
D.以上都不是
B
)
A.$CA$的长
B.$CD$的长
C.$CB$的长
D.以上都不是
答案:
B
4. 如上右图,直线$a$,$b被直线c$所截,$∠1与∠2$是 (
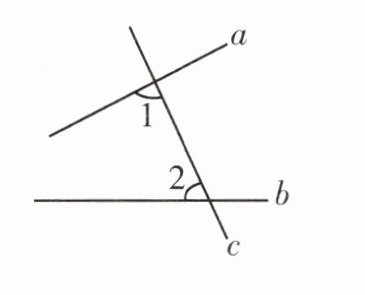
A.同位角
B.内错角
C.同旁内角
D.邻补角
C
)
A.同位角
B.内错角
C.同旁内角
D.邻补角
答案:
C
1. 已知$∠1与∠2$是对顶角,且$∠1与∠2$互为补角,那么$∠1 = $
90
$^{\circ}$.
答案:
90
2. 如下左图,$OC⊥AB$,$OD⊥OE$,图中与$∠1$互余的角有
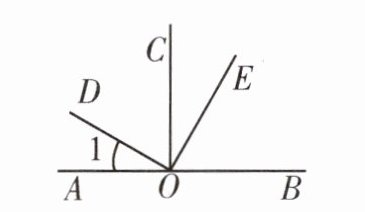
∠DOC,∠EOB
,若$∠COD = 60^{\circ}$,则$∠AOE = $120
$^{\circ}$.
答案:
∠DOC,∠EOB 120
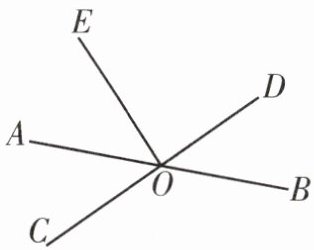
3. 如上右图,已知直线$AB$,$CD$,$EF相交于点O$,$∠1 = 95^{\circ}$,$∠2 = 53^{\circ}$,则$∠BOE$的度数为
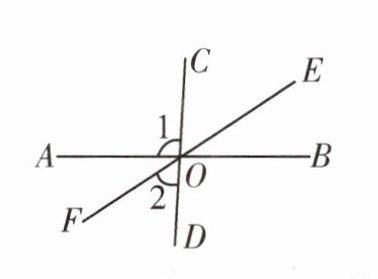
32°
.
答案:
32°
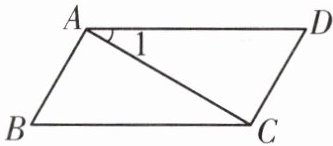
1. 如图,$∠1 = 30^{\circ}$,$∠B = 60^{\circ}$,$AB⊥AC$.
(1)$∠DAB + ∠B = $
(2)$AD与BC$平行吗?$AB与CD$平行吗? 试说明理由.
(1)$∠DAB + ∠B = $
180
$^{\circ}$.(2)$AD与BC$平行吗?$AB与CD$平行吗? 试说明理由.

答案:
1. 首先求$\angle DAB+\angle B$的值:
已知$AB\perp AC$,根据垂直的定义,$\angle BAC = 90^{\circ}$。
又已知$\angle1 = 30^{\circ}$,所以$\angle DAB=\angle1+\angle BAC=30^{\circ}+90^{\circ}=120^{\circ}$。
因为$\angle B = 60^{\circ}$,则$\angle DAB+\angle B=120^{\circ}+60^{\circ}=180^{\circ}$。
2. 然后判断$AD$与$BC$,$AB$与$CD$的平行关系:
判断$AD$与$BC$的平行关系**:
解:$AD// BC$,$AB$与$CD$不一定平行。
理由:因为$\angle DAB+\angle B = 180^{\circ}$(已证),根据“同旁内角互补,两直线平行”,所以$AD// BC$。
判断$AB$与$CD$的平行关系**:
仅根据已知条件$\angle1 = 30^{\circ}$,$\angle B = 60^{\circ}$,$AB\perp AC$,无法得到$AB$与$CD$平行的判定条件(如同位角相等、内错角相等或同旁内角互补等),所以$AB$与$CD$不一定平行。
综上,(1)$180$;(2)$AD// BC$,理由是同旁内角互补,两直线平行;$AB$与$CD$不一定平行,理由是不满足平行的判定条件。
已知$AB\perp AC$,根据垂直的定义,$\angle BAC = 90^{\circ}$。
又已知$\angle1 = 30^{\circ}$,所以$\angle DAB=\angle1+\angle BAC=30^{\circ}+90^{\circ}=120^{\circ}$。
因为$\angle B = 60^{\circ}$,则$\angle DAB+\angle B=120^{\circ}+60^{\circ}=180^{\circ}$。
2. 然后判断$AD$与$BC$,$AB$与$CD$的平行关系:
判断$AD$与$BC$的平行关系**:
解:$AD// BC$,$AB$与$CD$不一定平行。
理由:因为$\angle DAB+\angle B = 180^{\circ}$(已证),根据“同旁内角互补,两直线平行”,所以$AD// BC$。
判断$AB$与$CD$的平行关系**:
仅根据已知条件$\angle1 = 30^{\circ}$,$\angle B = 60^{\circ}$,$AB\perp AC$,无法得到$AB$与$CD$平行的判定条件(如同位角相等、内错角相等或同旁内角互补等),所以$AB$与$CD$不一定平行。
综上,(1)$180$;(2)$AD// BC$,理由是同旁内角互补,两直线平行;$AB$与$CD$不一定平行,理由是不满足平行的判定条件。
2. 如图,直线$AB$,$CD相交于点O$,$OA平分∠EOC$,且$∠DOE = 2∠AOC$,求证:$OE⊥CD$.
证明:∵∠DOE = 2∠AOC,OA 平分∠EOC,
∴∠DOE =
又∠DOE + ∠EOC = 180°,
∴∠DOE = ∠EOC =
∴OE⊥CD(

证明:∵∠DOE = 2∠AOC,OA 平分∠EOC,
∴∠DOE =
∠EOC
.又∠DOE + ∠EOC = 180°,
∴∠DOE = ∠EOC =
90°
.∴OE⊥CD(
垂直的定义
).
答案:
证明:
∵∠DOE = 2∠AOC,OA 平分∠EOC,
∴∠DOE = ∠EOC.
又∠DOE + ∠EOC = 180°,
∴∠DOE = ∠EOC = 90°.
∴OE⊥CD(垂直的定义).
∵∠DOE = 2∠AOC,OA 平分∠EOC,
∴∠DOE = ∠EOC.
又∠DOE + ∠EOC = 180°,
∴∠DOE = ∠EOC = 90°.
∴OE⊥CD(垂直的定义).
查看更多完整答案,请扫码查看


