《2025年全品学练考九年级数学上册人教版》

12. (12分)已知抛物线$y=a(x-1)^{2}+h$经过点$(0,-3)$和点$(3,0)$.
(1)求$a,h$的值;
(2)将该抛物线向上平移2个单位长度,再向右平移1个单位长度,得到新的抛物线,直接写出新的抛物线的函数解析式.

答案：
(1)$a=1,h=-4$
(2)$y=(x-2)^{2}-2$

13. (14分)已知二次函数$y=ax^{2}+k$的图象经过点$(-2,-3)$和点$(1,6)$.
(1)求这个二次函数的解析式;
(2)当$x$取何值时,$y$随$x$的增大而增大?当$x$取何值时,$y$随$x$的增大而减小?
(3)求这个函数的图象与$x$轴的交点坐标.

答案：
(1)$y=-3x^{2}+9$
(2)当$x＜0$时,$y$随$x$的增大而增大;
当$x＞0$时,$y$随$x$的增大而减小
(3)$(-\sqrt{3},0)$和$(\sqrt{3},0)$

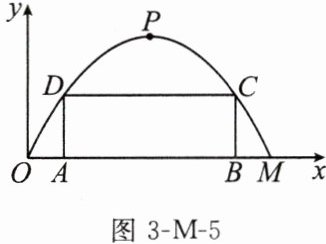
14. (14分)如图3-M-5,某隧道横截面的轮廓线是抛物线的一部分,最大高度为6米,底部宽度为12米.现以点$O$为原点,$OM$所在直线为$x$轴建立平面直角坐标系.
(1)直接写出点$M$及抛物线的顶点$P$的坐标;
(2)求出此抛物线的解析式;
(3)若要搭建一个矩形“支撑架”$AD-DC-CB$,使$C,D$两点在抛物线上,$A,B$两点在地面$OM$上,则“支撑架”总长的最大值是多少?

答案：
(1)$M(12,0),P(6,6)$
(2)$y=-\frac{1}{6}x^{2}+2x$
(3)15米