《2025年全品学练考九年级数学上册人教版》

11. (14分)如图9-M-9,在$\triangle ABC$中,$AB=AC$,以AB为直径的$\odot O$分别交AC,BC于点D,E.
(1)求证:$BE=CE$;
(2)若$AB=6,∠BAC=54^{\circ }$,求$\widehat {AD}$的长.

答案：
(1)略
(2)$ \frac{6}{5}\pi $

12. (14分)如图9-M-10,在$Rt\triangle ABC$中,$∠BAC=90^{\circ }$,以AB为直径作$\odot O$,交BC于点D,过点D作$\odot O$的切线交AC于点E.
(1)求证:$AE=CE$;
(2)已知$\odot O$的半径为$\sqrt {2}$,若$DE⊥AC$,求CD的长.

答案：
(1)证明:连接 $ OD $，$ AD $。
$ \because DE $ 与 $ \odot O $ 相切于点 $ D $，
$ \therefore \angle ODE = 90^{\circ} $，
$ \therefore \angle ODA + \angle ADE = 90^{\circ} $。
$ \because \angle BAC = 90^{\circ} $，
$ \therefore \angle OAD + \angle DAE = 90^{\circ} $。
$ \because OA = OD $，
$ \therefore \angle OAD = \angle ODA $，
$ \therefore \angle DAE = \angle ADE $，
$ \therefore AE = DE $。
同理可得 $ CE = DE $。
$ \therefore AE = CE $。
(2)2

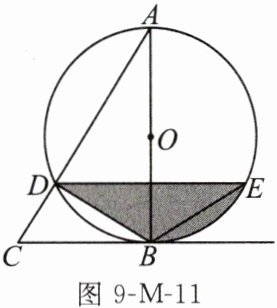
13. (18分)如图9-M-11,以$\triangle ABC$的边AB为直径作$\odot O$交边AC于点D,恰有$∠CBD=∠A$.
(1)求证:BC与$\odot O$相切.
(2)在$\odot O$上取一点E,使得$\widehat {BE}=\widehat {BD}$.
①求证:$DE// BC$;
②若$∠BED=30^{\circ },BD=6$,求阴影部分的面积.

答案：
(1)证明:$ \because AB $ 为 $ \odot O $ 的直径，
$ \therefore \angle ADB = 90^{\circ} $，
$ \therefore \angle A + \angle ABD = 90^{\circ} $。
又 $ \because \angle CBD = \angle A $，
$ \therefore \angle CBD + \angle ABD = 90^{\circ} $，
$ \therefore \angle ABC = 90^{\circ} $，
即 $ AB \perp BC $。
又 $ \because AB $ 为 $ \odot O $ 的直径，
$ \therefore BC $ 与 $ \odot O $ 相切。
(2)①证明:$ \because \overset{\frown}{BE} = \overset{\frown}{BD} $，
$ \therefore \angle A = \angle EDB $。
又 $ \because \angle CBD = \angle A $，
$ \therefore \angle CBD = \angle EDB $，
$ \therefore DE // BC $。
②$ 6\pi $