11. (12分)在如图6-M-9所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,三角形①②③均为顶点在格点上的三角形(每个小方格的顶点叫格点).结合图形解答下列问题:
(1)在图甲中,三角形①经过
(2)在图甲中,三角形③可以由三角形②经过一次旋转变换得到,其旋转中心是点
(3)在图乙中画出三角形①绕点A顺时针旋转$90^{\circ}$后得到的图形.

(1)在图甲中,三角形①经过
平移
变换(填“平移”或“旋转”或“轴对称”)可以得到三角形②;(2)在图甲中,三角形③可以由三角形②经过一次旋转变换得到,其旋转中心是点
A
(填“A”或“B”或“C”);(3)在图乙中画出三角形①绕点A顺时针旋转$90^{\circ}$后得到的图形.

答案:
(1)平移
(2)A
(3)略
(1)平移
(2)A
(3)略
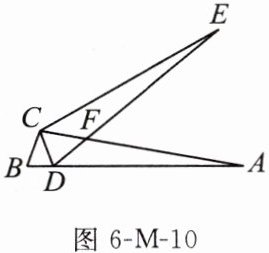
12. (14分)如图6-M-10,在$\triangle ABC$中,点D在AB边上,$CB = CD$,将边CA绕点C旋转到CE的位置,使得$\angle ECA = \angle DCB$,连接DE与CA交于点F,且$\angle B = 70^{\circ}$,$\angle A = 10^{\circ}$.
(1)求证:$AB = ED$;
(2)求$\angle AFE$的度数.
(1)求证:$AB = ED$;
(2)求$\angle AFE$的度数.

答案:
(1)略
(2)50°
(1)略
(2)50°
13. (20分)综合与实践
【问题情境】在综合与实践课上,老师出示了这样一个情境:
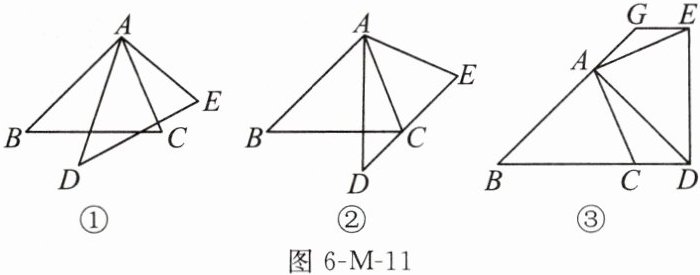
如图6-M-11,在$\triangle ABC$中,$AB = BC$,$AC \neq AB$,$\angle ABC = 45^{\circ}$,将$\triangle ABC$绕点A逆时针旋转得到$\triangle ADE$,点B,C的对应点分别是点D,E.
【初探感知】(1)如图①,$\angle E=$______$^{\circ}$;
【深入领悟】(2)如图②,当线段DE经过点C时,求证:$AD \perp BC$;
【融会贯通】(3)如图③,在旋转过程中,当点D落在BC的延长线上时,过点E作$EG // BD$,交BA的延长线于点G.请你判断线段AG和CD的数量关系,并说明理由.
【问题情境】在综合与实践课上,老师出示了这样一个情境:
如图6-M-11,在$\triangle ABC$中,$AB = BC$,$AC \neq AB$,$\angle ABC = 45^{\circ}$,将$\triangle ABC$绕点A逆时针旋转得到$\triangle ADE$,点B,C的对应点分别是点D,E.
【初探感知】(1)如图①,$\angle E=$______$^{\circ}$;
【深入领悟】(2)如图②,当线段DE经过点C时,求证:$AD \perp BC$;
【融会贯通】(3)如图③,在旋转过程中,当点D落在BC的延长线上时,过点E作$EG // BD$,交BA的延长线于点G.请你判断线段AG和CD的数量关系,并说明理由.

答案:
解:
(1)67.5
(2)证明:设AD与BC的交点为F,如图①.

由旋转的性质,得AE=AC,∠ACB=∠E=67.5°,∠ADE=∠ABC=45°,
∴∠ACE=∠E=67.5°,
∴∠BCE=135°,
∴∠DFC=∠BCE−∠ADE=135°−45°=90°,
∴AD⊥BC.
(3)AG=CD.理由:
如图②,延长BG,DE交于点H.

由旋转的性质,得AD=AB=DE=BC,∠ADE=∠ABC=45°,∠ACB=∠AED=67.5°,
∴∠ADB=∠ABC=45°,
∴∠BDE=90°,
∴∠H=45°=∠ABC,
∴∠GAE=∠AED−∠H=22.5°,HD=BD,
∴HD−DE=BD−BC,
即HE=CD.
∵EG//BD,
∴∠HGE=∠ABC=45°,
∴∠H=∠HGE,∠GEA=∠HGE−∠GAE=22.5°,
∴HE=GE、∠GEA=∠GAE,
∴GE=AG,
∴AG=CD.
解:
(1)67.5
(2)证明:设AD与BC的交点为F,如图①.

由旋转的性质,得AE=AC,∠ACB=∠E=67.5°,∠ADE=∠ABC=45°,
∴∠ACE=∠E=67.5°,
∴∠BCE=135°,
∴∠DFC=∠BCE−∠ADE=135°−45°=90°,
∴AD⊥BC.
(3)AG=CD.理由:
如图②,延长BG,DE交于点H.

由旋转的性质,得AD=AB=DE=BC,∠ADE=∠ABC=45°,∠ACB=∠AED=67.5°,
∴∠ADB=∠ABC=45°,
∴∠BDE=90°,
∴∠H=45°=∠ABC,
∴∠GAE=∠AED−∠H=22.5°,HD=BD,
∴HD−DE=BD−BC,
即HE=CD.
∵EG//BD,
∴∠HGE=∠ABC=45°,
∴∠H=∠HGE,∠GEA=∠HGE−∠GAE=22.5°,
∴HE=GE、∠GEA=∠GAE,
∴GE=AG,
∴AG=CD.
查看更多完整答案,请扫码查看


