《2025年全品学练考九年级数学上册人教版》

12. 如图 7-M-10,等腰三角形 ABC 的底角$∠C$为$70^{\circ }$,以腰 AB 为直径作半圆,交 BC 于点 D,交 AC 于点 E,则$\widehat {DE}$所对圆心角的度数为$40^{\circ }$.

答案： $ 40 ^ { \circ } $

13. 在半径为 4 cm 的$\odot O$中,弦 CD 平行于弦$AB,AB=4\sqrt {3}cm,∠COD=90^{\circ }$,则 AB 与 CD 之间的距离是$ ( 2 \sqrt { 2 } + 2 ) \mathrm { cm } $ 或 $ ( 2 \sqrt { 2 } - 2 ) \mathrm { cm } $.

答案： $ ( 2 \sqrt { 2 } + 2 ) \mathrm { cm } $ 或 $ ( 2 \sqrt { 2 } - 2 ) \mathrm { cm } $

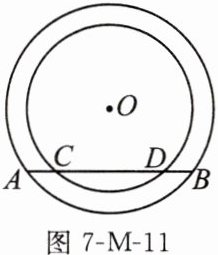
14. (12 分)如图 7-M-11,已知在以点 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于点 C,D.
(1)求证:$AC=BD;$
(2)若大圆的半径$R=10$,小圆的半径$r=8$,且圆心 O 到直线 AB 的距离为 6,求 AC 的长.

答案：
(1)略
(2)$ 8 - 2 \sqrt { 7 } $

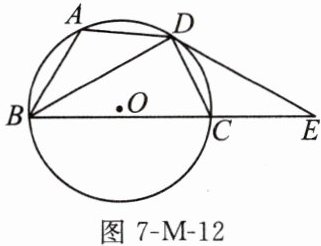
15. (14 分)如图 7-M-12,四边形 ABCD 内接于$\odot O$,D 是$\widehat {AC}$的中点,延长 BC 到点 E,使$CE=AB$,连接 BD,ED.
(1)求证:$BD=ED;$
(2)若$∠ABC=60^{\circ },AD=5$,求$\odot O$的半径.

答案：
(1)证明：
∵D是$ \overarc { A C } $的中点，
∴$ \overarc { A D } = \overarc { C D } $，
∴$ A D = C D $．
∵四边形ABCD内接于$ \odot O $，
∴$ \angle B A D + \angle B C D = 180 ^ { \circ } $．
又
∵$ \angle E C D + \angle B C D = 180 ^ { \circ } $，
∴$ \angle B A D = \angle E C D $．
在$ \triangle A B D $和$ \triangle C E D $中，
$ \left\{ \begin{array} { l } { A B = C E , } \\ { \angle B A D = \angle E C D , } \\ { A D = C D , } \end{array} \right. $
∴$ \triangle A B D \cong \triangle C E D ( \mathrm { SAS } ) $，
∴$ B D = E D $．
(2)5

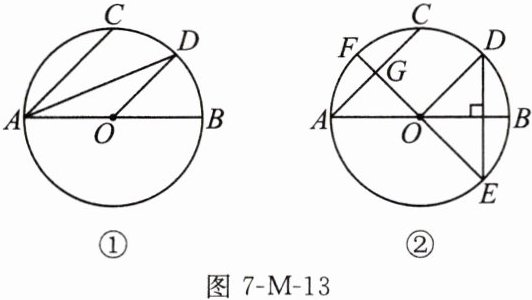
16. (17 分)如图 7-M-13,已知 AB 是$\odot O$的直径,点 C 在$\odot O$上,D 为$\widehat {BC}$的中点.
(1)如图①,连接 AC,AD,OD,求证:$OD// AC.$
(2)如图②,过点 D 作$DE⊥AB$交$\odot O$于点 E,直径 EF 交 AC 于点 G,若 G 为 AC 的中点,
①求证:$∠BOD=45^{\circ };$
②若$\odot O$的半径为 2,求 AC 的长.

答案：
(1)证明：
∵D为$ \overarc { B C } $的中点，
∴$ \overarc { B D } = \overarc { C D } $，
∴$ \angle B A D = \angle C A D $．
∵$ O A = O D $，
∴$ \angle B A D = \angle O D A $，
∴$ \angle C A D = \angle O D A $，
∴$ O D // A C $．
(2)①证明：
∵G为AC的中点，EF为直径，
∴$ E F \perp A C $．
∵$ O D // A C $，
∴$ D O \perp E F $，
∴$ \angle D O E = 90 ^ { \circ } $．
∵AB是$ \odot O $的直径，$ D E \perp A B $，
∴$ \overarc { B D } = \overarc { B E } $，
∴$ \angle B O D = \angle B O E = \frac { 1 } { 2 } \angle D O E = 45 ^ { \circ } $．
②$ 2 \sqrt { 2 } $